题目内容
2. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BD=3,CD=4,则$\frac{CD}{AD}$=$\frac{3}{4}$.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BD=3,CD=4,则$\frac{CD}{AD}$=$\frac{3}{4}$.
分析 由在Rt△ABC中,∠ACB=90°,CD⊥AB,根据同角的余角相等,可得∠ACD=∠B,又由∠CDB=∠ADC=90°,可证得△ACD∽△CBD,然后利用相似三角形的对应边成比例,即可求得答案.
解答 解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∵BD=3,CD=4,
∴$\frac{AD}{CD}$=$\frac{4}{3}$,
∴$\frac{CD}{AD}$=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 此题考查了相似三角形的判定与性质以及直角三角形的性质.此题难度不大,解题的关键是掌握有两角对应相等的三角形相似与相似三角形的对应边成比例定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点坐标是(1,3),则另一个交点的坐标是( )
| A. | (-1,-3) | B. | (-3,-1) | C. | (-1,-2) | D. | (-2,-3) |
11.蜡笔小新在公园中心雕像的北偏西25°的方向上,距离中心雕塑56厘米处,那么中心雕像的位置是在蜡笔小新的( )
| A. | 北偏东65°的方向,距离蜡笔小新56米处 | |
| B. | 东偏南25°的方向,距离蜡笔小新56米处 | |
| C. | 北偏西65°的方向,距离蜡笔小新56米处 | |
| D. | 南偏东25°的方向,距离蜡笔小新56米处 |
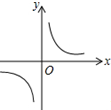

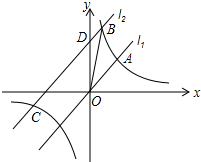 如图,直线l1:y=x与双曲线y=$\frac{k}{x}$相交于点A(3,a),将直线l1沿y轴向上平移8个单位单位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
如图,直线l1:y=x与双曲线y=$\frac{k}{x}$相交于点A(3,a),将直线l1沿y轴向上平移8个单位单位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点. 如图所示的两种瓷砖,如果只能用这两种瓷砖铺地,请你给出一个设计,使得铺出来的地面美丽大方.
如图所示的两种瓷砖,如果只能用这两种瓷砖铺地,请你给出一个设计,使得铺出来的地面美丽大方.