题目内容
8.已知m=2x-3,n=-x+6,若规定y=$\left\{\begin{array}{l}{2-m+n(m≥n)}\\{2+m-n(m<n)}\end{array}\right.$,则y的最大值为( )| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
分析 分类求函数解析式:若m≥n,即x≥3,于是y=-3x+11,根据一次函数的性质可得到当x=3时,y的最大值为2;若m<n,即x<3,于是得到y=3x-7,根据一次函数的性质可判断y没有最大值.
解答 解:若m≥n,即2x-3≥-x+6,解得x≥3,y=2-2x+3-x+6=-3x+11,当x=3时,y有最大值,最大值=-3×3+11=2;
若m<n,即2x-3<-x+6,解得x<3,y=2+2x-3+x-6=3x-7,y没有最大值,
所以y的最大值为2.
故选D.
点评 本题考查了一次函数与二元一次方程(组):由于任何一元一次方程都可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.也考查了一次函数的性质.

练习册系列答案
相关题目
18.某化肥厂把化肥送到甲、乙两个村庄,先后各送了两次.每次的运量和运费如表
试问两个村庄应该各负担运费多少元?(提醒:一吨化肥运往同一村庄的运费相同.)
| 次序 | 甲村运量(吨) | 乙村运量(吨) | 共计运费(元) |
| 第1次 | 6 | 5 | 270 |
| 第2次 | 8 | 11 | 490 |
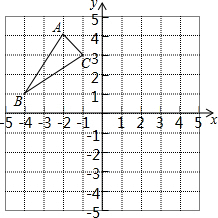 如图的方格纸中,△ABC的顶点坐标分别为A(-2,5),B(-4,1)和C (-1,3).
如图的方格纸中,△ABC的顶点坐标分别为A(-2,5),B(-4,1)和C (-1,3).