题目内容
8. 如图,已知AB∥CD,∠BAF=∠FED=21°,∠CDE=17°,则∠AFC=59°.
如图,已知AB∥CD,∠BAF=∠FED=21°,∠CDE=17°,则∠AFC=59°.
分析 在△CDE中由外角的性质可求得∠FCD,过点F作FG∥AB,可得到∠AFC=∠BAF+∠FCD,可求得答案.
解答  解:
解:
过F作FG∥AB,如图,
∵AB∥CD,
∴FG∥CD,
∴∠BAF=∠AFG,∠FCD=∠GFC,
∴∠AFC=∠BAF+∠FCD,
又∠FCD=∠FED+∠CDE=21°+17°=38°,
∴∠AFC=21°+38°=59°,
故答案为:59°.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
18.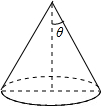 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )| A. | $\frac{5}{12}$ | B. | $\frac{5}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{12}{13}$ |
16.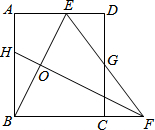 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
①∠AEB=∠BEF;②△BEF是等腰三角形;③△DEG与△BEF相似;④四边形ABCD的面积为56.
则以上正确的有( )
 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:①∠AEB=∠BEF;②△BEF是等腰三角形;③△DEG与△BEF相似;④四边形ABCD的面积为56.
则以上正确的有( )
| A. | ①③ | B. | ②③④ | C. | ①② | D. | ①②④ |
13.下列计算正确的是( )
| A. | 5ab-3ab=2 | B. | (1+$\sqrt{2}$)(1-$\sqrt{2}$)=1 | C. | -(-a)4÷a2=a2 | D. | (xy)-2=$\frac{1}{{x}^{2}{y}^{2}}$ |
20.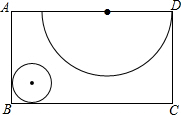 如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
 如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )| A. | 2πcm | B. | 3πcm | C. | $\sqrt{3}$πcm | D. | ($\sqrt{3}$+1)πcm |
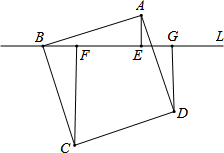 如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.
如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12. 将如图方格纸中的线段AB平移,分别画出经下列平移后所得的图形:
将如图方格纸中的线段AB平移,分别画出经下列平移后所得的图形: