题目内容
抛物线y=3（x+2）2-1中，当x 时，y随x的增大而减小；当x 时，y随x的增大而增大．
考点：二次函数的性质
专题：
分析：由解析式可求得对称轴为x=-2，且开口向上，可知在对称轴左侧y随x的增大而减小，在对称轴右侧y随x的增大而增大，可得出答案．
解答：解：∵y=3（x+2）2-1，
∴该二次函数开口向上，对称轴为x=-2，
当x＜-2时，y随x的增大而减小，当x＞-2时，y随x的增大而增大，
故答案为：＜-2；＞-2．
∴该二次函数开口向上，对称轴为x=-2，
当x＜-2时，y随x的增大而减小，当x＞-2时，y随x的增大而增大，
故答案为：＜-2；＞-2．
点评：本题主要考查二次函数的增减性，掌握在对称轴两侧的增减性相反是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列说法错误的是（ ）
| A、数轴上的点表示的数，右边的总比左边的数大 | ||
| B、|a|不可能是负数 | ||
C、-
| ||
| D、380000000用科学记数法表示3.8×108 |
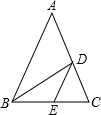如图，在△ABC中，AB=AC，D、E两点分别在AC、BC上，BD是∠ABC的平分线，DE∥AB，若BE=5cm，CE=3cm，则△CDE的周长是
如图，圆内接正五边形ABCDE的半径为2，连接AC、BD相交于点F．
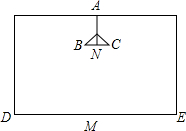在长、宽都为4m，高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡，为了集中光线，加上了灯罩（如图所示）．已知灯罩深AN=8m，灯泡离地面2m，为了使光线恰好照在墙角D、E处，灯罩的直径BC应为多少？（结果保留两位小数，
梅凯种子公司以一定价格销售“黄金1号”玉米种子，如果一次购买10千克以上（不含10千克）的种子，超过10千克的那部分种子的价格将打折，并依此得到付款金额y（单位：元）与一次购买种子数量x（单位：千克）之间的函数关系如图所示．下列四种说法：