题目内容
9. 如图,Rt△AOB的斜边长为5,一直角边OB长为4,则点A的坐标是(0,3),点B的坐标是(4,0).
如图,Rt△AOB的斜边长为5,一直角边OB长为4,则点A的坐标是(0,3),点B的坐标是(4,0).
分析 先根据OB=4求出B点坐标,再根据勾股定理求出OA的长,进而可得出A点坐标.
解答 解:∵点B在x轴正半轴上,OB=4,
∴B(4,0).
∵AB=5,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴A(0,3).
故答案为:(0,3),(4,0).
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.下列运算正确的是( )
| A. | (x+y)2=x2+y2 | B. | x2•x5=x10 | C. | x+y=2xy | D. | 2x3÷x=2x2 |
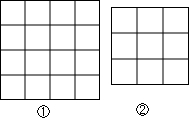 如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形: 如图是有几个小立方体块搭建成的几何体的俯视图,小正方体中的数字表示在该位置小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
如图是有几个小立方体块搭建成的几何体的俯视图,小正方体中的数字表示在该位置小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图. 已知,如图,折叠长方形的一边AD,使点D落在BC边上的点F处,如AB=8,BC=10.求EC的长.
已知,如图,折叠长方形的一边AD,使点D落在BC边上的点F处,如AB=8,BC=10.求EC的长.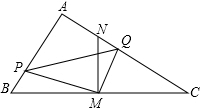 如图,在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,M是BC边的中点,MN⊥BC交AC于点N.直角∠PMQ绕顶点M旋转,使得边MP于线段BA交于点P,边MQ与线段AC交于点Q.
如图,在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,M是BC边的中点,MN⊥BC交AC于点N.直角∠PMQ绕顶点M旋转,使得边MP于线段BA交于点P,边MQ与线段AC交于点Q. 如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB-BA、CD-DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB-BA、CD-DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )


