题目内容
已知AB是半圆⊙O的直径,C是半圆⊙O上一点,且AC•BC=OC2,则∠CBA的度数等于 .
考点:圆的综合题,三角形的面积,圆周角定理,特殊角的三角函数值
专题:
分析:作CF⊥AB于F,连接OC,结合条件运用等积法可得OC2=AC•BC=AB•CF,由AB=2OC可得CF=
OC,从而可得∠COF=30°,根据圆周角定理可得∠CAB=15°,从而有∠CBA=75°.然后根据对称性可得到当点C在点C′(点C与点C′关于AB的垂直平分线对称)时的∠CBA的值,问题得以解决.
| 1 |
| 2 |
解答:解: 作CF⊥AB于F,连接OC,如图.
作CF⊥AB于F,连接OC,如图.
∵AB是半圆的直径,
∴∠ACB=90°,
∴S△ACB=
AC•BC=
AB•CF,
即AC•BC=AB•CF.
∵AC•BC=OC2,
∴OC2=AB•CF.
∵AB=2OC,
∴CF=
OC.
在Rt△OFC中,
∵sin∠COF=
=
,
∴∠COF=30°,
∴∠CAB=15°.
∴∠CBA=75°.
由对称性可知;当点C在点C′(点C与点C′关于AB的垂直平分线对称)时,∠CBA=15°.
故答案为:75°或15°.
 作CF⊥AB于F,连接OC,如图.
作CF⊥AB于F,连接OC,如图.∵AB是半圆的直径,
∴∠ACB=90°,
∴S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
即AC•BC=AB•CF.
∵AC•BC=OC2,
∴OC2=AB•CF.
∵AB=2OC,
∴CF=
| 1 |
| 2 |
在Rt△OFC中,
∵sin∠COF=
| CF |
| OC |
| 1 |
| 2 |
∴∠COF=30°,
∴∠CAB=15°.
∴∠CBA=75°.
由对称性可知;当点C在点C′(点C与点C′关于AB的垂直平分线对称)时,∠CBA=15°.
故答案为:75°或15°.
点评:本题考查了圆周角定理、三角形的面积公式、特殊角的三角函数值,考查了运用对称性解题,在解决问题的过程中,容易出现漏解的现象,需引起注意.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
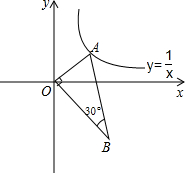 已知,如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点A在反比例函数y=
已知,如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点A在反比例函数y=