题目内容
2. 如图,菱形ABCD周长为8,∠BAD=120°,P为BD上一动点,E为CD中点,则PE+PC的最小值长为$\sqrt{3}$.
如图,菱形ABCD周长为8,∠BAD=120°,P为BD上一动点,E为CD中点,则PE+PC的最小值长为$\sqrt{3}$.
分析 先求出菱形各边的长度,作点E关于直线BD的对称点E′,连接CE′交BD于点P,则CE′的长即为PE+PC的最小值,由菱形的性质可知E′为AD的中点,由直角三角形的判定定理可得出△DCE′是直角三角形,利用勾股定理即可求出CE′的长.
解答 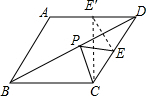 解:∵菱形ABCD的周长为8,
解:∵菱形ABCD的周长为8,
∴AD=DC=2,
作点E关于直线BD的对称点E′,连接CE′交BD于点P,则CE′的长即为PE+PC的最小值,
∵四边形ABCD是菱形,
∴BD是∠ADC的平分线,
∴E′在AD上,由图形对称的性质可知,DE=DE′=$\frac{1}{2}$AD=$\frac{1}{2}$×2=1,
∵DE′=DE=$\frac{1}{2}$DC,
∴△DCE′是直角三角形,
∴CE′=$\sqrt{C{D}^{2}-DE{′}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
故PE+PC的最小值是$\sqrt{3}$.
点评 本题考查的是轴对称-最短路线问题及菱形的性质、直角三角形的判定定理,根据轴对称的性质作出图形是解答此题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
12.分式$\frac{1}{{a}^{2}-9}$,$\frac{2}{{a}^{2}+6a+9}$,$\frac{5}{a-3}$的最简公分母是( )
| A. | (a+3)2(a-3) | B. | (a+3)2 | C. | (a+3)(a-3) | D. | (a-3)2(a+3)2 |
13.为了了解我市参加中考的75000名学生的视力情况,抽查了1000名学生的视力进行统计分析,下面四个判断中,正确的是( )
| A. | 75000名学生是总体 | |
| B. | 1000名学生的视力是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 上述调查是普查 |
17.某批篮球的质量检验结果如下:
(1)填写表中的空格;
(2)画出优等频率的折线统计图;
(3)从这批篮球中,任意抽取的一只篮球是优等品的概率的估计值是多少?
| 抽取的蓝球数n | 100 | 200 | 400 | 600 | 800 | 1000 | 1200 |
| 优等品频数m | 91 | 192 | 380 | 564 | 752 | 942 | 1128 |
| 优等品频率$\frac{m}{n}$ |
(2)画出优等频率的折线统计图;
(3)从这批篮球中,任意抽取的一只篮球是优等品的概率的估计值是多少?
14.分式$\frac{xy}{x+y}$中的x,y都扩大2倍,则分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 扩大4倍 | D. | 缩小2倍 |
11.分式方程$\frac{1}{x-1}=\frac{2}{x+1}$的解是( )
| A. | 1 | B. | -1 | C. | 无解 | D. | 3 |
 如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度AC=2cm,滑梯着地点B与梯架之间的距离BC=4cm.
如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度AC=2cm,滑梯着地点B与梯架之间的距离BC=4cm.