题目内容
13.若△ABC和△DEF满足下列条件,其中使△ABC与△DEF相似的是( )| A. | AB=6,BC=6,AC=9,DE=4,EF=4,DF=6 | |
| B. | AB=4,BC=6,AC=8,DE=5,EF=10,DF=15 | |
| C. | AB=1,BC=$\sqrt{2}$,AC=2,DE=$\sqrt{6}$,EF=$\sqrt{3}$,DF=$\sqrt{5}$ | |
| D. | AB=1,BC=$\sqrt{5}$,AC=3,DE=$\sqrt{15}$,EF=2$\sqrt{3}$,DF=$\sqrt{6}$ |
分析 根据相似三角形的判定定理进行判断.
解答 解:A、因为$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$=$\frac{3}{2}$,所以△ABC与△DEF相似,故本选项正确;
B、因为$\frac{AB}{DE}$≠$\frac{BC}{EF}$≠$\frac{AC}{DF}$,所以△ABC与△DEF不相似,故本选项错误;
C、因为$\frac{AB}{DE}$≠$\frac{BC}{EF}$≠$\frac{AC}{DF}$,所以△ABC与△DEF不相似,故本选项错误;
D、因为$\frac{AB}{DE}$≠$\frac{BC}{EF}$≠$\frac{AC}{DF}$,所以△ABC与△DEF不相似,故本选项错误;
故选:A.
点评 本题考查了相似三角形的判定,考查了相似三角形各对应边长比例均相等的性质.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
18.对于方程3x2-x-2=0,下列判断正确的是( )
| A. | 一次项系数为1 | B. | 常数项是2 | C. | 二次项系数是3x2 | D. | 一次项是-x |
5.关于x的一元二次方程x2+x+1=0的根的情况是( )
| A. | 有两个不相等的正根 | B. | 有两个不相等的负根 | ||
| C. | 没有实数根 | D. | 有两个相等的实数根 |
2.计算|2-$\sqrt{5}$|+|4-$\sqrt{5}$|的值是( )
| A. | -2 | B. | 2 | C. | 2$\sqrt{5}$-6 | D. | 6-2$\sqrt{5}$ |
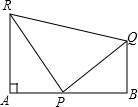 如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度.
如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度. 如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点A的坐标是(3,$\sqrt{3}$).
如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点A的坐标是(3,$\sqrt{3}$).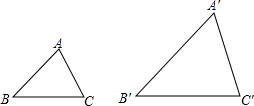 如图,已知△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,若AB=6,BC=5,AC=4,求△A′B′C′的周长.
如图,已知△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,若AB=6,BC=5,AC=4,求△A′B′C′的周长.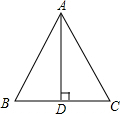 在△ABC中,AB=AC,AD是底边上的高,如图,若AC=6cm,AD=5cm,求BD的值.(精确到0.01cm)
在△ABC中,AB=AC,AD是底边上的高,如图,若AC=6cm,AD=5cm,求BD的值.(精确到0.01cm)