题目内容
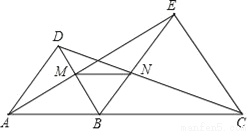
在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.
接着张老师又让学生分小组进行探究:你还能得出什么结论?
精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.
创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

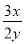 B.
B. 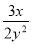 C.
C. 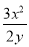 D.
D. 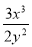
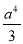 ,
, 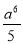 ,
, 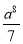 ,…,则第2 017个式子是( )
,…,则第2 017个式子是( )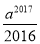 B.
B. 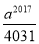 C.
C. 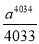 D.
D. 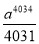
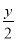 +1=0
+1=0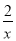 +3=0 D. 2y2=8
+3=0 D. 2y2=8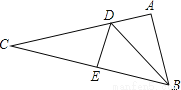
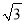 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米)