题目内容
8. 如图,△ABC中,∠B=40°,∠C=62°,AD⊥BC于点D,AE平分∠BAC,则∠DAE的度数是11°.
如图,△ABC中,∠B=40°,∠C=62°,AD⊥BC于点D,AE平分∠BAC,则∠DAE的度数是11°.
分析 根据三角形的内角和定理,可求得∠BAC的度数,由AE是∠BAC的平分线,可得∠EAC的度数;在直角△ADC中,可求出∠DAC的度数,所以∠DAE=∠EAC-∠DAC,即可得出.
解答 解:∵△ABC中,∠B=40°,∠C=62°,
∴∠BAC=180°-∠B-∠C
=180°-40°-62°
=78°,
∵AE是∠BAC的平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=39°,
∵AD是BC边上的高,
∴在直角△ADC中,
∠DAC=90°-∠C=90°-62°=28°,
∴∠DAE=∠EAC-∠DAC=39°-28°=11°,
故答案为:11°
点评 本题主要考查了三角形的内角和定理和三角形的高、角平分线的性质,学生应熟练掌握三角形的高、中线和角平分线这些基本知识,能灵活运用解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18. 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=29°30′,则下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=29°30′,则下列结论错误的是( )
 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=29°30′,则下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=29°30′,则下列结论错误的是( )| A. | ∠ACD=119°30′ | B. | ∠ACD=∠BCE | C. | ∠ACE=150°30′ | D. | ∠ACE-∠BCD=120° |
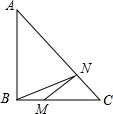 如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为5.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为5. 如图,在△ABC中,点D在BC边上,△ABD绕点A旋转后与△ACE重合,如果∠ECB=100°,那么旋转角的大小是80°.
如图,在△ABC中,点D在BC边上,△ABD绕点A旋转后与△ACE重合,如果∠ECB=100°,那么旋转角的大小是80°. 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,则⊙O的半径为5.
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,则⊙O的半径为5. 如图,在△ABC中,∠C=90°,BD是∠ABC的平分线且BD=4.若BC=3,则点D到AB的距离是$\sqrt{7}$.
如图,在△ABC中,∠C=90°,BD是∠ABC的平分线且BD=4.若BC=3,则点D到AB的距离是$\sqrt{7}$.