题目内容
4.在平面直角坐标系中,点A(2,m+1)和点B(-m+3,-4)都在直线l上且直线l∥x轴.(1)求A、B两点间的距离;
(2)若过点P(-1,2)的直线l′与直线l垂直于点C,求垂足点C的坐标.
分析 (1)利用与x轴平行的直线上所有点的纵坐标相同得到m+1=-4,解得m=-5,易得A(2,-4),B(-2,-4),计算A,B两点间的横坐标之差即可;
(2)由于直线l′与直线l垂直于点C,则直线l′平行y轴,于是可得C点的横坐标为-1,加上直线l上的纵坐标都为-4,于是可得C点坐标.
解答 解:(1)∵直线l∥x轴,
∴m+1=-4,解得m=-5,
∴A(2,-4),B(-2,-4),
∴A,B两点间的距离=2-(-2)=4;
(2)∵直线l′与直线l垂直于点C,
∴直线l′平行y轴,
∴C点的横坐标为-1,
而直线l上的纵坐标都为-4,
∴C(-1,-4).
点评 本题考查了坐标与图形性质,利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系是解决问题的关键.

练习册系列答案
相关题目
 已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),I(3,-2),J(2,0),K(3,2),L(1,1)
已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),I(3,-2),J(2,0),K(3,2),L(1,1)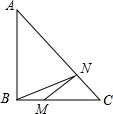 如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为5.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,点M在BC上,且BM=1,N是AC上一动点,则BN+MN的最小值为5.