题目内容
14.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=3a-1}\\{x+2y=2}\end{array}\right.$的解满足x+y=1,则a的值为$\frac{2}{3}$.分析 方程组中两方程相加表示出x+y,代入x+y=1中计算即可求出a的值.
解答 解:$\left\{\begin{array}{l}{2x+y=3a-1①}\\{x+2y=2②}\end{array}\right.$,
①+②得:3(x+y)=3a+1,即x+y=a+$\frac{1}{3}$,
代入x+y=1中得:a+$\frac{1}{3}$=1,
解得:a=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
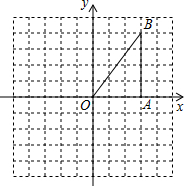 如图,在平面直角坐标系xOy中,已知点B(3,4),BA⊥x轴于A.
如图,在平面直角坐标系xOy中,已知点B(3,4),BA⊥x轴于A.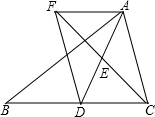 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.



