题目内容
5.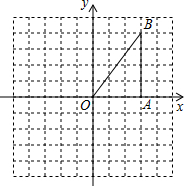 如图,在平面直角坐标系xOy中,已知点B(3,4),BA⊥x轴于A.
如图,在平面直角坐标系xOy中,已知点B(3,4),BA⊥x轴于A.(1)画出将△OAB绕原点O逆时针旋转90°后所得的△OA1B1,并写出点B的对应点B1的坐标为(-4,3);
(2)在(1)的条件下,连接BB1,则线段BB1的长度为5$\sqrt{2}$.
分析 (1)根据网格结构找出点A1、B1的位置,然后与点O顺次连接即可,再根据平面直角坐标系写出点B1的坐标;
(2)利用勾股定理列式计算即可得解.
解答 解:(1)如图.
点B1(-4,3);
(2)由勾股定理得,BB1=$\sqrt{{7}^{2}+{1}^{2}}$=5$\sqrt{2}$.
故答案为:(-4,3);5$\sqrt{2}$.
点评 本题考查了利用旋转变换作图,勾股定理,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
15.对分式$\frac{1}{2({a}^{2}-9)}$,$\frac{3}{4({a}^{2}+6a+9)}$通分时,最简公分母是( )
| A. | 4(a-3)(a+3)2 | B. | 4(a2-9)(a2+6a+9) | C. | 8(a2-9)(a2+6a+9) | D. | 4(a-3)2(a+3)2 |
13.在平面直角坐标平面内,点P到x轴的距离是5,到y轴的距离是3,并且点P在第四象限,则点P的坐标是( )
| A. | (3,-5) | B. | (5,-3) | C. | (-3,5) | D. | (-3,5)或(3,-5) |
10.据外汇局网站5月16日消息:国家外汇管理局统计数据显示,2016年4月,银行结售汇逆差1534亿元人民币,其中“1534亿”用科学记数法表示为( )
| A. | 1.534×103 | B. | 1.534×1011 | C. | 15.34×108 | D. | 1534×108 |
 如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).
如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4). 如图Rt△ACB中,已知∠BAC=30°,BC=2,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE. EF⊥AB,垂足为F,连接DF.
如图Rt△ACB中,已知∠BAC=30°,BC=2,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE. EF⊥AB,垂足为F,连接DF.