题目内容
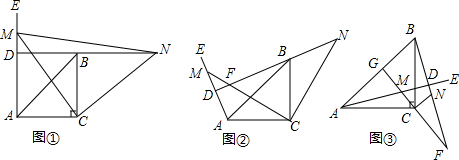
1.如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.(1)问题发现:直接写出∠NDE=90度;
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.
(3)如图③,若∠EAC=15°,BD=$\sqrt{2}$,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
分析 (1)根据题意证明△MAC≌△NBC即可;
(2)∠NDE的大小不变,证明△MAC≌△NBC,得到∠N=∠AMC,又∠MFD=∠NFC,所以∠MDF=∠FCN=90°,即∠NDE=90°.
(3)先证明△MAC≌△NBC,所以∠NBC=∠MAC=15°,再证明∠BDH=∠ACH=90°,∠ABD=60°,求出AB=2$\sqrt{2}$,根据AC=AB•cos45°,即可解答.
解答 解:(1)∵∠ACB=90°,∠MCN=90°,
∴∠ACM=∠BCN,
在△MAC和△NBC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACM=∠BCN}\\{MC=NC}\end{array}\right.$,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=90°,
又∵∠ACB=90°,∠EAC=90°,
∴∠NDE=90°.
故答案为:90.
(2)∠NDE的大小不变,
在△MAC和△NBC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACM=∠BCN}\\{MC=NC}\end{array}\right.$,
∴△MAC≌△NBC,
∴∠N=∠AMC,
又∵∠MFD=∠NFC,
∴∠MDF=∠FCN=90°,
即∠NDE=90°.
(3)AC=2,
在△MAC和△NBC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACM=∠BCN}\\{MC=NC}\end{array}\right.$,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=15°,
如图③,设BC与AD交于点H,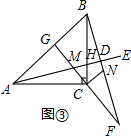
又∵∠AHC=∠BHD,
∴∠BDH=∠ACH=90°,
∴在Rt△ABD中,∠ABD=∠ABC+∠NBC=45°+15°=60°
∵BD=$\sqrt{2}$,
∴AB=2$\sqrt{2}$,
∴AC=AB•cos45°=2.
点评 本题考查了全等三角形的性质定理与判定定理,三角形的内角和,解决本题的关键是证明△MAC≌△NBC.

 每课必练系列答案
每课必练系列答案| A. |  | B. |  | C. |  | D. |  |
 解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.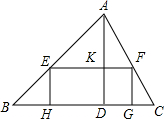 如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.
如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.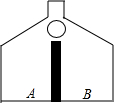 现有一游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物后,等可能地向左、右两边落下.
现有一游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物后,等可能地向左、右两边落下. 如图,?ABCD中,O为BC边上一点,OD平分∠ADC,以O为圆心,OC为半径画圆,交OD于点E,若AB=6,?ABCD的面积是42$\sqrt{3}$,$\widehat{EC}$=π,请判断直线AB与⊙O的位置关系,并说明理由.
如图,?ABCD中,O为BC边上一点,OD平分∠ADC,以O为圆心,OC为半径画圆,交OD于点E,若AB=6,?ABCD的面积是42$\sqrt{3}$,$\widehat{EC}$=π,请判断直线AB与⊙O的位置关系,并说明理由.