题目内容
3.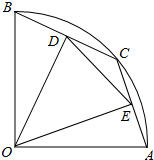 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
分析 (1)如图(1),根据垂径定理可得BD=$\frac{1}{2}$BC,然后只需运用勾股定理即可求出线段OD的长;
(2)连接AB,如图(2),用勾股定理可求出AB的长,根据垂径定理可得D和E分别是线段BC和AC的中点,根据三角形中位线定理就可得到DE=$\frac{1}{2}$AB,DE保持不变;
解答 解:(1)如图(1),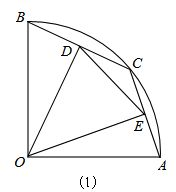
∵OD⊥BC,
∴BD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∵∠BDO=90°,OB=5,BD=3,
∴OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=4,
即线段OD的长为4.
(2)存在,DE保持不变.
理由:连接AB,如图(2),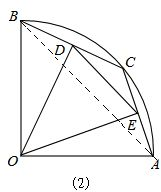
∵∠AOB=90°,OA=OB=5,
∴AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=5$\sqrt{2}$,
∵OD⊥BC,OE⊥AC,
∴D和E分别是线段BC和AC的中点,
∴DE=$\frac{1}{2}$AB=$\frac{5\sqrt{2}}{2}$,
∴DE保持不变.
点评 本题考查了垂径定理、三角形中位线定理、等腰三角形的性质、三角函数、勾股定理等知识,运用垂径定理及三角形中位线定理是解决第(2)小题的关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
18.△ABC是⊙O内接三角形,∠BOC=80°,那么∠A等于( )
| A. | 80° | B. | 40° | C. | 140° | D. | 40°或140° |
8.某同学用一扇形纸片为玩偶制作了一个圆锥形帽子(不考虑接缝),已知扇形的半径为13cm,扇形的弧长为10π cm,那么这个圆锥形帽子的高是( )
| A. | 5cm | B. | 12cm | C. | 13cm | D. | 14cm |
 、
、 拼出至少两个对称图形.(画在以下方框内)
拼出至少两个对称图形.(画在以下方框内)
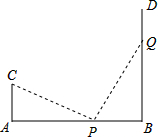 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动4分钟后△CAP与△PQB全等.
如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动4分钟后△CAP与△PQB全等.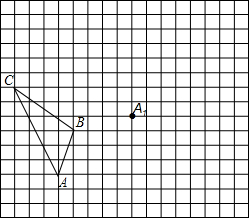 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.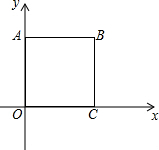 如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:$\sqrt{2}$,点A的坐标为(0,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).
如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:$\sqrt{2}$,点A的坐标为(0,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).