题目内容
13.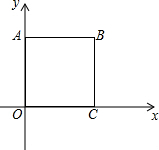 如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:$\sqrt{2}$,点A的坐标为(0,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).
如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:$\sqrt{2}$,点A的坐标为(0,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).
分析 由题意可得OA:OD=1:$\sqrt{2}$,又由点A的坐标为(1,0),即可求得OD的长,又由正方形的性质,即可求得E点的坐标.
解答 解:∵正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:$\sqrt{2}$,
∴OA:OD=1:$\sqrt{2}$,
∵点A的坐标为(0,1),
即OA=1,
∴OD=$\sqrt{2}$,
∵四边形ODEF是正方形,
∴DE=OD=$\sqrt{2}$.
∴E点的坐标为:($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).
故答案为:($\sqrt{2}$,$\sqrt{2}$)或(-$\sqrt{2}$,-$\sqrt{2}$).
点评 此题考查了位似变换的性质与正方形的性质.此题比较简单,注意理解位似变换与相似比的定义是解此题的关键.

练习册系列答案
相关题目
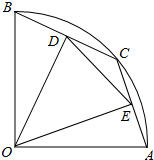 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.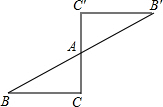 如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点A中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为$\frac{4\sqrt{3}}{3}$.
如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点A中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为$\frac{4\sqrt{3}}{3}$. 如图,AC平分∠BAF,∠B=80°,∠C=50°,求证:EF∥BC.
如图,AC平分∠BAF,∠B=80°,∠C=50°,求证:EF∥BC.