题目内容
12. 如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,求该图形的面积.
如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,求该图形的面积.
分析 连接AC,在Rt△ACD中,AD=8,CD=6,根据勾股定理可求AC;在△ABC中,由勾股定理的逆定理可证△ABC为直角三角形,利用两个直角三角形的面积差求图形的面积.
解答 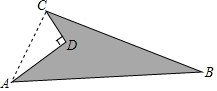 解:连接AC,在Rt△ACD中,AD=8,CD=6,
解:连接AC,在Rt△ACD中,AD=8,CD=6,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=10,
在△ABC中,
∵AC2+BC2=102+242=262=AB2,
∴△ABC为直角三角形;
∴图形面积为:
S△ABC-S△ACD=$\frac{1}{2}$×10×24-$\frac{1}{2}$×6×8=96.
点评 本题考查了勾股定理及其逆定理的运用,三角形面积的求法,关键是得到△ABC为直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
 如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )| A. | 16cm2 | B. | 20cm2 | C. | 80cm2 | D. | 160cm2 |
1.下列说法中正确的是( )
| A. | 面积相等的两个三角形全等 | |
| B. | 斜边和一直角边对应相等的两个直角三角形全等 | |
| C. | 两个等腰直角三角形全等 | |
| D. | 一边和一个内角对应相等的两个等腰三角形全等 |
2.“事件可能发生”是指( )
| A. | 事件一定会发生 | B. | 事件也许会发生,也许不会发生 | ||
| C. | 事件发生的机会很大 | D. | 事件发生的可能性是$\frac{1}{2}$ |

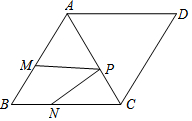 已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$.
已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$.