题目内容
在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B,D作BE⊥PA,DF⊥PA,垂足分别为E,F,如图①.
(1)请探究BE,DF,EF这三条线段的长度具有怎样的数量关系?若点P在DC的延长线 上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别
上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别 直接写出结论.
直接写出结论.
(2)就(1)中的三个结论选择一个加以证明.
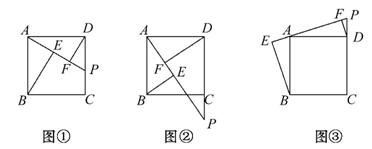
【解析】(1)在图①中,BE, DF,EF这三条线段长度具有这样的数量关系:BE-DF=EF;
DF,EF这三条线段长度具有这样的数量关系:BE-DF=EF;
在图②中,BE,DF,EF这三条线段长度具有这样的数量关系:DF-BE=EF;
在图③中,BE,DF,EF这三条线段长度具有这样的数量关系:DF+BE=EF.
(2)答案不唯一.对图①中结论证明如下:
∵BE⊥PA,DF⊥PA,∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,∴△BAE≌△ADF,∴BE=AF,AE=DF,
∵AF-AE=EF,∴BE-DF=EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
100名学生进行20秒钟跳绳测试,测试成绩统计如表(跳绳的个数用x表示):
| x | 20<x ≤30 | 30<x ≤40 | 40<x ≤50 | 50<x ≤60 | 60<x ≤70 | x>70 |
| 人数 | 5 | 2 | 13 | 31 | 23 | 26 |
则这次测试成绩的中位数m满足( )
A.40<m≤50 B.50<m≤60
C.60<m≤70 D.m>70


 A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .
A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .
 的一元二次方程
的一元二次方程 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数 的取值范围是( )
的取值范围是( )  B.
B. 且
且 C.
C.  且
且 是一元二次方程,则
是一元二次方程,则 .
. ,对角线AE,DF相交于点O,连接OC.求OC的长度.(5分)
,对角线AE,DF相交于点O,连接OC.求OC的长度.(5分)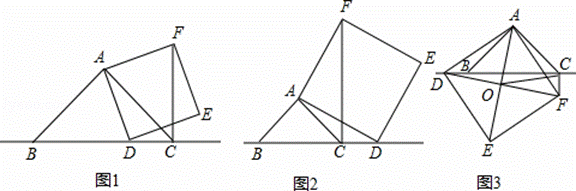
 ____________________
____________________