题目内容
已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;(6分)
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;(2分)
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;(2分)新 课 标 第 一 网
②若正方形ADEF的边长为2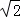 ,对角线AE,DF相交于点O,连接OC.求OC的长度.(5分)
,对角线AE,DF相交于点O,连接OC.求OC的长度.(5分)
.证明:(1)∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
则在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∵BD+CD=BC,
∴CF+CD=BC;
(2)CF﹣CD=BC;
(3)①CD﹣CF=BC
②∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,

∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD,
∵∠ABC=45°,
∴∠ABD=135°,
∴∠ACF=∠ABD=135°,
∴∠FCD=90°,
∴△FCD是直角三角形.
∵正方形ADEF的边长为2 且对角线AE、DF相交于点O.
且对角线AE、DF相交于点O.
∴DF= AD=4,O为DF中点.
AD=4,O为DF中点.
∴OC= DF=2.
DF=2.

如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )
| A.60° | B.90° | C.120° | D.150° |


 上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别
上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别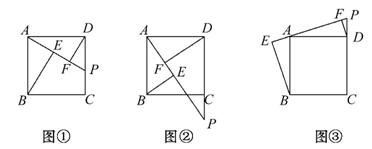

 有两个不相等的实数根.(10分)
有两个不相等的实数根.(10分) 的平方根是±4
的平方根是±4  根等于平方根的数是1
根等于平方根的数是1 的相反数就是它本身,乙说:一个数
的相反数就是它本身,乙说:一个数 的倒数也等于它本身,则
的倒数也等于它本身,则 .
.