题目内容
已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+1)x+k(k+1)=0 的两个实数根,第三边BC的长为5.
(1)k为何值时,△ABC是以BC为斜边的直角三角形?
(2)k为何值时,△ABC是等腰三角形?并求△ABC的周长.
(1)k为何值时,△ABC是以BC为斜边的直角三角形?
(2)k为何值时,△ABC是等腰三角形?并求△ABC的周长.
考点:一元二次方程的应用
专题:
分析:(1)根据题意得出AB、AC的长,再由根与系数的关系得出k的值;
(2)根据等腰三角形的性质,分三种情况讨论:①AB=AC,②AB=BC,③BC=AC;后两种情况相同,则可有另种情况,再由根与系数的关系得出k的值.
(2)根据等腰三角形的性质,分三种情况讨论:①AB=AC,②AB=BC,③BC=AC;后两种情况相同,则可有另种情况,再由根与系数的关系得出k的值.
解答:解:(1)∵△ABC是以BC为斜边的直角三角形,BC=5,
∴AB2+AC2=25,
∵AB、AC的长是关于x的一元二次方程x2-(2k+1)x+k(k+1)=0的两个实数根,
∴AB+AC=2k+1,AB•AC=k2+k,
∴AB2+AC2=(AB+AC)2-2AB•AC,
即(2k+1)2-2(k2+k)=25,
整理,得
(k-3)(k+4)=0
解得k=3或-4(不合题意舍去).
即当k=3时,△ABC是以BC为斜边的直角三角形;
(2)∵△ABC是等腰三角形;
∴当AB=AC时,△=b2-4ac=0,
∴(2k+1)2-4(k2+k)=0
解得k不存在;
当AB=BC时,即AB=5,
∴5+AC=2k+1,5AC=k2+k,
解得k=5或4,
∴AC=6或4
∴△ABC的周长为16或14.
∴AB2+AC2=25,
∵AB、AC的长是关于x的一元二次方程x2-(2k+1)x+k(k+1)=0的两个实数根,
∴AB+AC=2k+1,AB•AC=k2+k,
∴AB2+AC2=(AB+AC)2-2AB•AC,
即(2k+1)2-2(k2+k)=25,
整理,得
(k-3)(k+4)=0
解得k=3或-4(不合题意舍去).
即当k=3时,△ABC是以BC为斜边的直角三角形;
(2)∵△ABC是等腰三角形;
∴当AB=AC时,△=b2-4ac=0,
∴(2k+1)2-4(k2+k)=0
解得k不存在;
当AB=BC时,即AB=5,
∴5+AC=2k+1,5AC=k2+k,
解得k=5或4,
∴AC=6或4
∴△ABC的周长为16或14.
点评:本题考查了解一元二次方程的方法,以及实际应用,注意分论讨论思想.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在直角坐标系内,已知A、B两点的坐标分别为A(0,1)、B(3,2),M为x轴上一点,且MA+MB最小,则M的坐标是( )
| A、(0,0) |
| B、(1,0) |
| C、(2,0) |
| D、(3,0) |
 如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.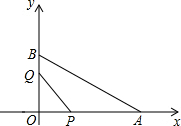 如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么:
如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么: