题目内容
16.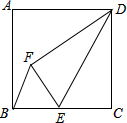 如图,在边长为12的正方形ABCD中,点E是边BC的中点,将△DCE沿DE折叠,点C落在正方形内的点F处,则△BEF的面积为$\frac{72}{5}$.
如图,在边长为12的正方形ABCD中,点E是边BC的中点,将△DCE沿DE折叠,点C落在正方形内的点F处,则△BEF的面积为$\frac{72}{5}$.
分析 延长EF交AB于点G,连接GD,过点B作BH⊥EF,垂足为H.由折叠得到结论,用HL判断出Rt△DAG≌Rt△DFG,设AG=FG=x,则EG=x+6,BG=12-x,
在△BEG中,依据勾股定理列方程可求得x的值,接下来,在△BEG中,利用面积法可求得BH的长,最后应用三角形面积公式求解即可.
解答 解:如图所示:延长EF交AB于点G,连接GD,过点B作BH⊥EF,垂足为H.
由折叠可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,$\left\{\begin{array}{l}{AD=DF}\\{DG=DG}\end{array}\right.$,
∴Rt△DAG≌Rt△DFG,
∵正方形边长是12,
∴BE=EC=EF=6,
设AG=FG=x,则EG=x+6,BG=12-x,
由勾股定理得:EG2=BE2+BG2,
即:(x+6)2=62+(12-x)2,
解得:x=4,
∴AG=GF=4,BG=8,GE=10,
∴BH=$\frac{BG•BE}{GE}$=$\frac{6×8}{10}$=$\frac{24}{5}$.
∴S△BEF=$\frac{1}{2}$EF•BH=$\frac{1}{2}$×6×$\frac{24}{5}$=$\frac{72}{5}$.
故答案为:$\frac{72}{5}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用、全等三角形的判定,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标为( )
| A. | (3,3)或(6,-6) | B. | (3,-3)或 (6,-6) | C. | (3,3) | D. | (3,-3) |
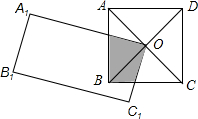 如图正方形ABCD的边长为2,对角线AC、BD相交于点O,点O又是长方形A1B1C1O的一个顶点,且OA1=4,OC1=2,使长方形绕点O转动过程中,长方形和正方形重叠部分的面积是1.
如图正方形ABCD的边长为2,对角线AC、BD相交于点O,点O又是长方形A1B1C1O的一个顶点,且OA1=4,OC1=2,使长方形绕点O转动过程中,长方形和正方形重叠部分的面积是1.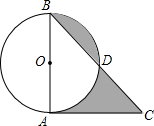 如图,AB是⊙O的直径,BD是弦,过点A的切线交BD延长线于点C.若AB=AC=4,则图中阴影部分图形的面积和是4.
如图,AB是⊙O的直径,BD是弦,过点A的切线交BD延长线于点C.若AB=AC=4,则图中阴影部分图形的面积和是4.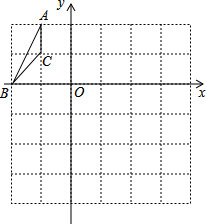 如图,△ABC在平面直角坐标系中,以原点O为位似中心,将△ABC放大到原来的2倍得到△A′B′C′,那么落在第四象限的点A′的坐标是(2,-4).
如图,△ABC在平面直角坐标系中,以原点O为位似中心,将△ABC放大到原来的2倍得到△A′B′C′,那么落在第四象限的点A′的坐标是(2,-4).