题目内容
17.已知P(x,y)是平面直角坐标系上的一个点,且它的横、纵坐标是一次方程组$\left\{\begin{array}{l}5x+2y=11a+18\\ 2x-3y=12a-8\end{array}\right.$(a为任意实数)的解,则当a变化时,点P一定不会经过( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 首先用含有a的代数式表示出x、y的值,然后分析x、y不能同时为负数得到其不会经过第三象限.
解答 解:解方程组得:$\left\{\begin{array}{l}{x=3a+2}\\{y=-2a+4}\end{array}\right.$,
∵当x=3a+2<0时,解得:a<-$\frac{2}{3}$,
∴此时y=-2a+4>0,
∴当x<0时y>0,
∴点P一定不会经过第三象限,
故选C.
点评 本题考查了一次函数与二元一次方程的知识,解题的关键是首先用含有a的代数式表示出x、y的值.

练习册系列答案
相关题目
2.在下列实数$\frac{1}{4}$,$\sqrt{5}$,$-\sqrt{7}$,3.14,π.其中有理数出现的频率为( )
| A. | 20% | B. | 40% | C. | 60% | D. | 80% |
9.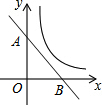 如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
 如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.分式方程$\frac{1}{3x}$=$\frac{1}{2x}$+2的解为( )
| A. | x=$\frac{1}{2}$ | B. | x=$-\frac{1}{12}$ | C. | x=$\frac{1}{12}$ | D. | x=-12 |
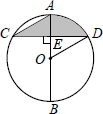 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠C=30°,CD=2$\sqrt{3}$.则阴影部分的面积S阴影=$\frac{2π}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠C=30°,CD=2$\sqrt{3}$.则阴影部分的面积S阴影=$\frac{2π}{3}$.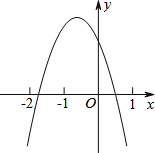 在平面直角坐标系中,如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标为x1、x2,其中-2<x1<-1,0<x2<1,则下列结论:
在平面直角坐标系中,如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标为x1、x2,其中-2<x1<-1,0<x2<1,则下列结论: 第一次模拟考试后,数学科陈老师把一班的数学成绩制成如图的统计图(图中每组数据包含横轴上左边的数据不含右边的数据),并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8.
第一次模拟考试后,数学科陈老师把一班的数学成绩制成如图的统计图(图中每组数据包含横轴上左边的数据不含右边的数据),并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8. 如图,已知∠ABC、∠DEF,且AB∥DE,BC∥EF,∠B、∠E具有怎样的关系?说明理由.
如图,已知∠ABC、∠DEF,且AB∥DE,BC∥EF,∠B、∠E具有怎样的关系?说明理由.