题目内容
7.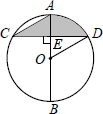 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠C=30°,CD=2$\sqrt{3}$.则阴影部分的面积S阴影=$\frac{2π}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠C=30°,CD=2$\sqrt{3}$.则阴影部分的面积S阴影=$\frac{2π}{3}$.
分析 根据垂径定理求得CE=ED=$\sqrt{3}$,然后由圆周角定理知∠DOE=60°,然后通过解直角三角形求得线段OD、OE的长度,最后将相关线段的长度代入S阴影=S扇形ODA-S△DOE+S△AEC.
解答 解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=$\sqrt{3}$,
又∵∠DCA=30°,
∴∠DOE=2∠ACD=60°,∠ODE=30°,
∴OE=DE•cot60°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,OD=2OE=2,
∴S阴影=S扇形ODA-S△DOE+S△AEC=$\frac{60π×O{C}^{2}}{360}$-$\frac{1}{2}$OE×ED+$\frac{1}{2}$AE•EC=$\frac{2π}{3}$-$\frac{1}{3}\sqrt{3}$+$\frac{1}{2}\sqrt{3}$=$\frac{2π}{3}$.
故答案为$\frac{2π}{3}$.
点评 本题考查了垂径定理、扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.

练习册系列答案
相关题目
2.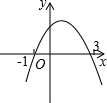 如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之间,与y轴相交于正半轴:①b=a+c;②a+b>0;③2a+b>0;④$\frac{{b}^{2}-4ac}{4a}$+a+b+c<0中,正确结论的个数是( )
如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之间,与y轴相交于正半轴:①b=a+c;②a+b>0;③2a+b>0;④$\frac{{b}^{2}-4ac}{4a}$+a+b+c<0中,正确结论的个数是( )
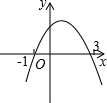 如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之间,与y轴相交于正半轴:①b=a+c;②a+b>0;③2a+b>0;④$\frac{{b}^{2}-4ac}{4a}$+a+b+c<0中,正确结论的个数是( )
如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之间,与y轴相交于正半轴:①b=a+c;②a+b>0;③2a+b>0;④$\frac{{b}^{2}-4ac}{4a}$+a+b+c<0中,正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.在下列实数:$\frac{1}{3}$,$\sqrt{2}$,-$\sqrt{3}$,π,3.14中任取一个,取到有理数的概率为( )
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
 如图,将图案绕点O按逆时针方向旋转90°,得到的图案是( )
如图,将图案绕点O按逆时针方向旋转90°,得到的图案是( )



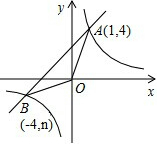 已知,如图,反比例函数$y=\frac{k}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)、B(-4,n),
已知,如图,反比例函数$y=\frac{k}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)、B(-4,n),