题目内容
2.已知关于x的一元二次方程x2+2mx-1+m2=0.(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值.
分析 (1)根据a=1,b=2m,c=-1+m2,求出△=b2-4ac的值,进而作出判断;
(2)把x=1代入方程列出m的一元二次方程,因式分解法解方程即可.
解答 (1)证明:∵a=1,b=2m,c=-1+m2,
∴△=b2-4ac=(2m)2-4(-1+4m2)=4>0,
∴对于任意实数m,方程总有两个不相等的实数根;
(2)当x=1时,m2+2m=0,
解得m等于0或-2.
点评 本题主要考查了根的判别式以及一元二次方程的解的知识,解答本题的关键是掌握根的判别式△与根个数的关系以及解一元二次方程的方法步骤,此题难度不大.

练习册系列答案
相关题目
10.下列实数中,是无理数的是( )
| A. | $\frac{11}{7}$ | B. | 0.1010010001 | C. | $\root{3}{9}$ | D. | 0 |
17.抛物线y=x2-2x-3与x轴的交点为A,B,则AB=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.下列说法错误的是( )
| A. | 48°21′36″的余角是41.64° | |
| B. | 点C是线段AB上的点,AB=10,AC=6,点D是线段BC的中点,则线段CD=2 | |
| C. | ∠AOC=60°,经过顶点O引一条射线OD,且∠AOD=25°,则∠COD=85° | |
| D. | 已知线段a,b如图 ,则尺规作图中 ,则尺规作图中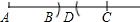 ,线段AD=2a-b ,线段AD=2a-b |
11.已知点P(2+m,n-3)与点Q(m,1+n)关于原点对称,则m-n的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
 射击比赛中,某队员的10次设计成绩如图所示,估计他的平均成绩是9环.
射击比赛中,某队员的10次设计成绩如图所示,估计他的平均成绩是9环.