题目内容
11. 如图,在正方形ABCD中,BC=2,E是对角线BD上的一点,且BE=AB,求△EBC的面积.
如图,在正方形ABCD中,BC=2,E是对角线BD上的一点,且BE=AB,求△EBC的面积.
分析 作EF⊥BC于F,则∠EFB=90°,由正方形的性质得出AB=BC=2,∠DAB=∠ABC=90°,∠ABD=∠DBC=45°,得出△BEF是等腰直角三角形,因此EF=BF,由勾股定理得出EF=BF=$\frac{\sqrt{2}}{2}$BE=$\sqrt{2}$,△EBC的面积=$\frac{1}{2}$BC•EF,即可得出结果.
解答 解:作EF⊥BC于F,如图所示: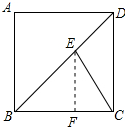
则∠EFB=90°,
∵四边形ABCD是正方形,
∴AB=BC=2,∠DAB=∠ABC=90°,
∴∠ABD=∠DBC=$\frac{1}{2}$∠ABC=45°,
∴△BEF是等腰直角三角形,
∴EF=BF,
∵BE=AB,
∴BE=BC=2,
∴EF=BF=$\frac{\sqrt{2}}{2}$BE=$\sqrt{2}$,
∴△EBC的面积=$\frac{1}{2}$BC•EF=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、勾股定理、三角形面积的计算方法;熟练掌握正方形的性质,通过作辅助线得出△BEF是等腰直角三角形是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
1.已知点M(3,-4),那么M到原点的距离是( )
| A. | 3 | B. | 4 | C. | -4 | D. | 5 |
6.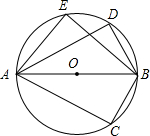 如图,已知AB是⊙O的直径,C,D,E是⊙O上的三个点,在下列各组角中,相等的是( )
如图,已知AB是⊙O的直径,C,D,E是⊙O上的三个点,在下列各组角中,相等的是( )
 如图,已知AB是⊙O的直径,C,D,E是⊙O上的三个点,在下列各组角中,相等的是( )
如图,已知AB是⊙O的直径,C,D,E是⊙O上的三个点,在下列各组角中,相等的是( )| A. | ∠C和∠D | B. | ∠DAB和∠CAB | C. | ∠C和∠EBA | D. | ∠DAB和∠DBE |
1.下列等式正确的是( )
| A. | -|3|=|-3| | B. | |3|=|-3| | C. | |-3|=-3 | D. | -(-3)=-|-3| |
 如图,∠C=∠1,∠2与∠D互余,BE⊥DF,垂足为G.求证:AB∥CD.
如图,∠C=∠1,∠2与∠D互余,BE⊥DF,垂足为G.求证:AB∥CD.