题目内容
17．已知点P（a+1，2a-3）关于x轴的对称点在第一象限，则a的取值范围在数轴上表示正确的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 求出P点在第四象限，得出不等式组，求出不等式组的解集，即可得出选项．
解答 解：∵点P（a+1，2a-3）关于x轴的对称点在第一象限，
∴点P在第四象限，
∴$\left\{\begin{array}{l}{a+1＞0}\\{2a-3＜0}\end{array}\right.$，
解得：-1＜a＜$\frac{3}{2}$，
在数轴上表示为：
，
故选A．
点评 本题考查了关于x轴、y轴对称的点的坐标，解一元一次不等式组，在数轴上表示不等式组的解集的应用，能根据题意得出不等式组是解此题的关键．
练习册系列答案
相关题目
8．
如图，AB和CD是⊙O的两条直径，弦DE∥AB，∠DOE=50°，那么∠BOD为（ ）
如图，AB和CD是⊙O的两条直径，弦DE∥AB，∠DOE=50°，那么∠BOD为（ ）| A． | 115° | B． | 100° | C． | 80° | D． | 65° |
5．抛物线y=（x-5）2+6的对称轴是（ ）
| A． | 直线x=-5 | B． | 直线x=5 | C． | 直线x=-6 | D． | 直线x=6 |
12．下列二次根式中，是最简二次根式的是（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{12}$ | C． | $\sqrt{\frac{1}{2}}$ | D． | $\sqrt{{x}^{4}+{x}^{2}{y}^{2}}$ |
2．估计$\sqrt{6}$的值在（ ）
| A． | 2到3之间 | B． | 3到4之间 | C． | 4到5之间 | D． | 5到6之间 |
9．根据分式的基本性质，分式$\frac{-a}{a-2b}$可变形为（ ）
| A． | $\frac{a}{a+2b}$ | B． | $\frac{a}{-a-2b}$ | C． | $-\frac{a}{a+2b}$ | D． | $-\frac{a}{a-2b}$ |
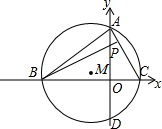如图，在平面直角坐标系中，A（0，6），P（0，4），点C为x轴正半轴上任一点，BP⊥AC交x轴于B点，△ABC内接于⊙M交y轴负半轴于D点．
7．
如图，直线AB∥CD，AF交CD于点E，AG平分∠FAB，∠CEF=140°，则∠GAB等于（ ）
如图，直线AB∥CD，AF交CD于点E，AG平分∠FAB，∠CEF=140°，则∠GAB等于（ ）| A． | 35° | B． | 20° | C． | 45° | D． | 50° |