题目内容
2. 如图,BP是△ABC的内角∠ABC的角平分线,交外角∠ACD的角平分线CP于点P,已知∠A=70°,则∠P的度数为35°.
如图,BP是△ABC的内角∠ABC的角平分线,交外角∠ACD的角平分线CP于点P,已知∠A=70°,则∠P的度数为35°.
分析 根据角平分线的定义可得∠CBP=$\frac{1}{2}$∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠PCE,然后整理即可得到∠P=$\frac{1}{2}$∠BAC,代入数据计算即可得解.
解答 解:∵BP平分∠ABC,
∴∠CBP=$\frac{1}{2}$∠ABC,
∵CP平分△ABC的外角,
∴∠PCE=$\frac{1}{2}$∠ACE=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
在△BCP中,由三角形的外角性质,∠PCE=∠CBP+∠P=$\frac{1}{2}$∠ABC+∠P,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠P,
∴∠P=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×70°=35°.
故答案为:35°.
点评 本题考查了三角形的内角和,三角形的外角性质的应用,能正确运用性质进行推理和计算是解此题的关键,注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.同学小明在用一副三角板画出了许多不同度数的角,但下列哪个度数他画不出来( )
| A. | 135° | B. | 120° | C. | 75° | D. | 25° |
14.2014年四川旅游局公布了四川各城市宣传语中英文对照,成华区的宣传口号中有这样一句:“生态城区,现代成华”,它的英文宣传语为“Ecological District,Modem Chenhua”.在路边一块由这个32个英文字母牌拼成的宣传栏上,一只小鸟停留在字母“o”的字母牌上的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{5}{32}$ | D. | $\frac{3}{32}$ |
12.一汽车租赁公司拥有某种型号的汽车50辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数y(辆)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接判断每月租出的车辆数y(辆)与每辆车的月租金x(元)之间满足三类函数关系中的哪类函数关系,并求出y与x之间的关系式(写出自变量x的取值范围).
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
| x | … | 10800 | 11000 | 11200 | 11400 | … |
| y | … | 30 | 25 | 20 | 15 | … |
(2)已知租出的车每辆每月需要维护费200元,未租出的车每辆每月需要维护费40元.则每月租出的车共需要维护费200(-$\frac{1}{40}$x+300)元(用含x的代数式表示,不必化简),每月未租出的车共需要维护费40[50-(-$\frac{1}{40}$x+300)]元(用含x的代数式表示,不必化简).现设该租赁公司每月扣除所有车辆的维护费后获得的月收益为W元,若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得的月收益W最大?并求出公司的最大月收益是多少元.
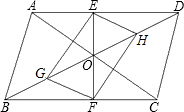 如图,在?ABCD中,对角线AC、BD相交于点O,已知E、F、G、H分别是BC、AD、OB、OD的中点,试说明四边形EGFH是平行四边形.
如图,在?ABCD中,对角线AC、BD相交于点O,已知E、F、G、H分别是BC、AD、OB、OD的中点,试说明四边形EGFH是平行四边形.