题目内容
已知y=(m-2)xm2-m+3x+6是二次函数,则m= ,顶点坐标是 ,当x 时,函数值随x的增大而减小.
考点:二次函数的性质,二次函数的定义
专题:
分析:根据二次函数的最高指数是2,二次项系数不等于0列方程求出m,然后整理成顶点式形式,再写出顶点坐标;最后根据二次函数的增减性解答.
解答:解:由题意得,m2-m=2且m-2≠0,
解得m=-1,m=2,且m≠2,
所以,m=-1,
二次函数解析式为y=-3x2+3x+6=-3(x2-x+
)+
+6,
=-3(x-
)2+
,
所以,顶点坐标(
,
),当x>
时,函数值随x的增大而减小.
故答案为:-1;(
,
),>
.
解得m=-1,m=2,且m≠2,
所以,m=-1,
二次函数解析式为y=-3x2+3x+6=-3(x2-x+
| 1 |
| 4 |
| 3 |
| 4 |
=-3(x-
| 1 |
| 2 |
| 27 |
| 4 |
所以,顶点坐标(
| 1 |
| 2 |
| 27 |
| 4 |
| 1 |
| 2 |
故答案为:-1;(
| 1 |
| 2 |
| 27 |
| 4 |
| 1 |
| 2 |
点评:本题考查了二次函数的性质,二次函数的定义,把函数解析式整理成顶点式形式求解更简便.

练习册系列答案
相关题目
抛物线y=x2+bx+c向左平移2个单位,再向下平移3个单位后得到抛物线y=x2-2x+1,则( )
| A、b=-6,c=12 |
| B、b=-8,c=-14 |
| C、b=6,c=12 |
| D、b=-8,c=14 |
抛物线y=2(x+1)2-1的顶点坐标是( )
| A、(-1,1) |
| B、(1,-1) |
| C、(-1,-1) |
| D、(1,1) |
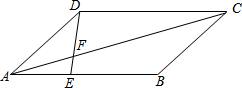 已知如图:?ABCD中,AE:EB=1:2,S△AEF=6cm2
已知如图:?ABCD中,AE:EB=1:2,S△AEF=6cm2 如图,若AO=OB,∠1=∠2,加上条件
如图,若AO=OB,∠1=∠2,加上条件