题目内容
9.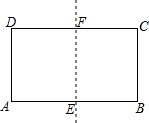 将矩形ABCD沿两条较长边的中点对折得到矩形ADFE,若矩形ADFE∽矩形ABCD,且AB=4,则AD的长等于( )
将矩形ABCD沿两条较长边的中点对折得到矩形ADFE,若矩形ADFE∽矩形ABCD,且AB=4,则AD的长等于( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 根据相似多边形的对应边成比例得到比例式,代入已知数据进行计算即可.
解答 解:∵矩形ADFE∽矩形ABCD,
∴$\frac{DF}{AD}$=$\frac{AD}{AB}$,即$\frac{\frac{1}{2}AB}{AD}$=$\frac{AD}{AB}$,
解得AD=2$\sqrt{2}$.
故选:D.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边成比例是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.圆周长公式C=2πR中,下列说法正确的是( )
| A. | π、R是变量,2为常量 | B. | C、R为变量,2、π为常量 | ||
| C. | R为变量,2、π、C为常量 | D. | C为变量,2、π、R为常量 |
17.已知α为锐角,sinα+cosα的值为( )
| A. | 小于1 | B. | 大于1 | C. | 等于1 | D. | 不能确定 |
1.n边形的内角和等于1080°,则n的值是( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
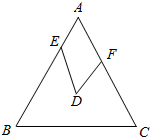 如图,已知点D是边长为1的等边三角形ABC的内心,点E,F分别在边AB,AC上,且满足∠EDF=60°,求△AEF的周长.
如图,已知点D是边长为1的等边三角形ABC的内心,点E,F分别在边AB,AC上,且满足∠EDF=60°,求△AEF的周长.
 实数a,b在数轴上对应的位置如图示:
实数a,b在数轴上对应的位置如图示: