题目内容
13.若关于x的方程$\frac{2k}{x+2}-\frac{x-1}{{{x^2}+2x}}=\frac{kx+1}{x}$只有一个解(相等的解也算作一个),求k的值.分析 首先去分母、去括号、把方程化成一般形式,然后分成方程是一元一次方程和一元二次方程两种情况进行讨论,当是一个一元一次方程时只有一个解;当时一元二次方程时,△=0只有一个解;当△>0时,方程有一个解是增根时也只有一个解.
解答 解:原分式方程可化为kx2+2x+1=0.(x≠0,x≠-2)①
(1)当k=0时,x=-$\frac{1}{2}$是分式方程的一个解.
(2)当k≠0时,△=22-4k=0时,k=1,x=-1是分式方程的一个解.
(3)当k≠0时,△>0时,方程①的两个根一个是分式方程的增根,另一个是分式方程的根.
当x=-2是分式方程的增根时,代入方程①得k(x-2)2+2×(-2)+1=0,
则k=$\frac{3}{4}$.
此时,方程①的另一个根$x=-\frac{2}{3}$是分式方程的一个解;
当x=0是分式方程的增根时,代入方程①得k×02+2×0+1=0不可能成立.
故k的值是0或1或$\frac{3}{4}$.
点评 本题考查了分式方程的解,注意到当△>0时,方程有一个解是增根时也只有一个解是本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1.用一个平面去截正方体,截面不可能是( )
| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |
18.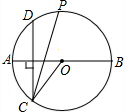 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )| A. | 到CD的距离保持不变 | B. | 到D点距离保持不变 | ||
| C. | 等分$\widehat{BD}$ | D. | 位置不变 |
3.已知点M(a,3),B(2,b)关于x轴对称,则a+b的值( )
| A. | -5 | B. | 5 | C. | -1 | D. | 1 |
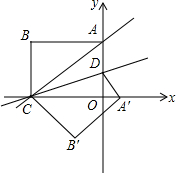 如图,矩形AOCB在直角坐标系中,O为原点,C在x轴上,A在y轴上,直线AC的关系式为y=$\frac{3}{4}$x+9,D是OA上的一点,若将矩形AOCB沿CD折叠,点A恰好落在x轴上的A′处.
如图,矩形AOCB在直角坐标系中,O为原点,C在x轴上,A在y轴上,直线AC的关系式为y=$\frac{3}{4}$x+9,D是OA上的一点,若将矩形AOCB沿CD折叠,点A恰好落在x轴上的A′处.