题目内容
 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.(1)若∠ABC=60°,则∠ADC=
(2)BE与DF平行吗?试说明理由.
考点:平行线的判定与性质
专题:常规题型
分析:(1)根据四边形内角和为360°可计算出∠ADC=120°,再根据角平分线定义得到∠FDA=
ADC=60°,然后利用互余可计算出∠AFD=30°;
(2)先根据BE平分∠ABC交CD于E得∠ABE=
∠ABC=30°,而∠AFD=30°则∠ABE=∠AFD,于是可根据平行线的判定方法得到BE∥DF.
| 1 |
| 2 |
(2)先根据BE平分∠ABC交CD于E得∠ABE=
| 1 |
| 2 |
解答:解:(1)∵∠A=∠C=90°,∠ABC=60°,
∴∠ADC=360°-∠A-∠C-∠ABC=120°,
∵DF平分∠ADC交AB于F,
∴∠FDA=
ADC=60°,
∴∠AFD=90°-∠ADF=30°;
故答案为120,30;
(2)BE∥DF.理由如下:
∵BE平分∠ABC交CD于E,
∴∠ABE=
∠ABC=
×60°=30°,
∵∠AFD=30°;
∴∠ABE=∠AFD,
∴BE∥DF.
∴∠ADC=360°-∠A-∠C-∠ABC=120°,
∵DF平分∠ADC交AB于F,
∴∠FDA=
| 1 |
| 2 |
∴∠AFD=90°-∠ADF=30°;
故答案为120,30;
(2)BE∥DF.理由如下:
∵BE平分∠ABC交CD于E,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AFD=30°;
∴∠ABE=∠AFD,
∴BE∥DF.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
计算
-
的结果是( )
| (-4)2 |
| 3 | 8 |
| A、2 | B、±2 | C、-2或0 | D、0 |
若已知分式
的值为0,则m的值为( )
| m-1 |
| m2-1 |
| A、1 | B、±1 |
| C、不能确定 | D、不存在 |
 如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点.
如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点.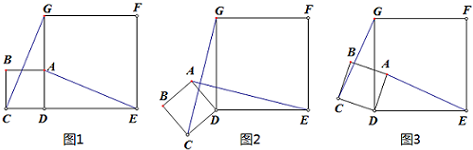
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,设D为BC上任意一点,点D不与B、C重合,且DC=x,若三角形ABD的面积为y.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,设D为BC上任意一点,点D不与B、C重合,且DC=x,若三角形ABD的面积为y.