题目内容
7.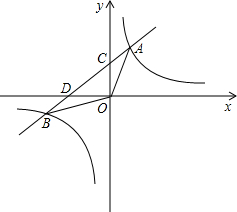 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-3,0),A点的横坐标是3,tan∠CDO=$\frac{1}{3}$.
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-3,0),A点的横坐标是3,tan∠CDO=$\frac{1}{3}$.(1)求一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的解析式;
(2)点M为第一象限双曲线上的一个动点,是否存在以M、A、D、O为顶点的四边形是平行四边形?若存在,求M点的坐标;若不存在,请说明理由.
分析 (1)过A作AE⊥x轴于点E,由三角函数的定义可求得A点坐标,再利用待定系数法可求得一次函数和反比例函数的解析式;
(2)由题意可知OD=AM,可求得M点的坐标,再把M点的坐标代入反比例函数解析式进行验证即可.
解答 解:
(1)如图,过A作AE⊥x轴于点E,则∠AED=90°,OE=6,
∵D(-3,0),
∴OD=3,
∴DE=OD+OE=6,
在Rt△AED中,∠AED=90°,
∴tan∠ADE=$\frac{AE}{DE}$,
∵tan∠CDO=tan∠ADE=$\frac{1}{3}$,
∴AE=DE•tan∠ADE=$\frac{1}{3}$×6=2,
∴A(3,2),
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象过点A,
∴k=3×2=6,
∴反比例函数解析式为y=$\frac{6}{x}$,
∵一次函数y=ax+b经过A、D两点,
∴$\left\{\begin{array}{l}{3a+b=2}\\{-3a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=1}\end{array}\right.$,
∴一次函数解析式为y=$\frac{1}{3}$x+1;
(2)不存在.
∵点M为第一象限双曲线上的一个动点,
∴以点A、D、O、M为顶点的平行四边形为平行四边形ADOM,
即AM∥OD,AM=OD,
∵A(3,2),D(-3,0),
∴OD=AM=3,
∴M(6,2),
当x=6时,y=$\frac{6}{6}$=1≠2,
∴点M不在双曲线上,这与点M为第一象限双曲线上的一个动点相矛盾,
∴不存在满足条件的点M.
点评 本题为反比例函数的综合应用,涉及待定系数法、三角函数的定义、平行四边形的性质等知识.在(1)中求得A点的坐标是解题的关键,在(2)中利用平行四边形的性质求得M点的坐标是解题的关键.本题考查知识点较多,综合性较强,但难度不大,较易得分.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案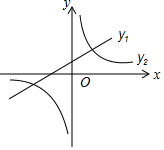 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于(2,m)和(n,-1)两点,观察图象,下列判断正确的是( )
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于(2,m)和(n,-1)两点,观察图象,下列判断正确的是( )| A. | 当x>2时,y1<y2 | B. | 当x<2时,y1<y2 | C. | 当x>n时,y1<y2 | D. | 当x<n时,y1<y2 |
| A. | 7×105 | B. | 7×106 | C. | 70×106 | D. | 7×107 |
| A. | x2•x2•x2 | B. | x2+x2+x2 | C. | x2•x3 | D. | x4+x2 |
| A. | 2a+3b=5ab | B. | (-2a2)3=-8a6 | C. | a6÷a2=a3 | D. | ($\frac{1}{2}$)0=0 |
 如图,已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
如图,已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
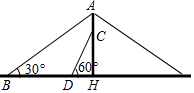 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732) 如图,⊙O的内接正三角形ABC的边心距OD为2cm,则⊙O的半径为4cm.
如图,⊙O的内接正三角形ABC的边心距OD为2cm,则⊙O的半径为4cm.