题目内容
(1)如图1,在△ABC中,∠BAC=2∠B,∠BAD=∠DAC.说明:∠BAD=∠B.
(2)如图2,已知点E在BA延长线上,∠EAD=∠CAD,∠B=∠C.说明:AD∥BC.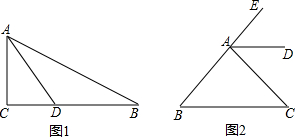
(2)如图2,已知点E在BA延长线上,∠EAD=∠CAD,∠B=∠C.说明:AD∥BC.

考点:平行线的判定
专题:证明题
分析:(1)先根据∠BAD=∠DAC可知∠BAC=2∠BAD,再由∠BAC=2∠B即可得出结论;
(2)根据三角形外角的性质可知∠B+∠C=2∠EAC,再由∠B=∠C得出∠B=
∠EAC,根据∠EAD+∠CAD=∠EAC,∠EAD=∠CAD可知∠EAD=
∠EAC,通过等量代换即可得出结论.
(2)根据三角形外角的性质可知∠B+∠C=2∠EAC,再由∠B=∠C得出∠B=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵∠BAD=∠DAC,
∴∠BAC=2∠BAD,
∵∠BAC=2∠B,
∴∠BAD=∠B;
(2)证明:∵∠B+∠C=2∠EAC,∠B=∠C,
∴∠B=
∠EAC,
∵∠EAD+∠CAD=∠EAC,∠EAD=∠CAD,
∴∠EAD=
∠EAC,
∴∠B=∠EAD,
∴AD∥BC.
∴∠BAC=2∠BAD,
∵∠BAC=2∠B,
∴∠BAD=∠B;
(2)证明:∵∠B+∠C=2∠EAC,∠B=∠C,
∴∠B=
| 1 |
| 2 |
∵∠EAD+∠CAD=∠EAC,∠EAD=∠CAD,
∴∠EAD=
| 1 |
| 2 |
∴∠B=∠EAD,
∴AD∥BC.
点评:本题考查的是平行线的判定,用到的知识点为:同位角相等,两直线平行.

练习册系列答案
相关题目
通过尺规作图作一个角的平分线的理论依据是( )
| A、SAS | B、SSS |
| C、ASA | D、AAS |
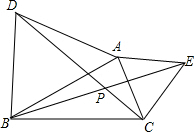 如图,已知△ABD和△AEC中,AD=AB,AE=AC,∠DAB=∠EAC=60°,CD、BE相交于点P.
如图,已知△ABD和△AEC中,AD=AB,AE=AC,∠DAB=∠EAC=60°,CD、BE相交于点P.