题目内容
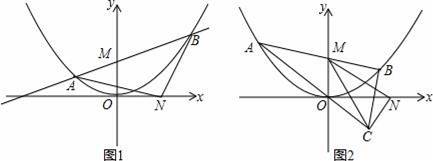
如图1,动直线l:y=kx+2交抛物线y=
 x2于A、B两点(A在B的左边),交y轴于M点,N为x轴正半轴上一点,且ON=OM+1
x2于A、B两点(A在B的左边),交y轴于M点,N为x轴正半轴上一点,且ON=OM+1
(1)直接写出M、N两点的坐标
(2)如图1,连AN、BN,当∠ANB=90°时,求k的值;如图2,过B作y轴的平行线交直线OA于C,试探求△MNC的周长的最小值.

【考点】二次函数综合题.
【分析】(1)首先求得直线与y轴的交点M的坐标,然后根据ON=OM+1求得点N的坐标;
(2)设A(x1,
 x12),B(x2,
x12),B(x2,
 x22),A,B分别作x轴的垂线,垂足分别为D,E,利用△ADN∽△NEB列出比例式求得有关两点坐标的方程,利用根与系数的关系列式求解即可;求得直线AO的解析式,然后确定点C的位置,然后利用轴对称的性质确定三角形的面积的最小值即可.
x22),A,B分别作x轴的垂线,垂足分别为D,E,利用△ADN∽△NEB列出比例式求得有关两点坐标的方程,利用根与系数的关系列式求解即可;求得直线AO的解析式,然后确定点C的位置,然后利用轴对称的性质确定三角形的面积的最小值即可.
【解答】解:(1)M(0,2),N(3,0);
(2)设A(x1,
 x12),B(x2,
x12),B(x2,
 x22),
x22),
过A,B分别作x轴的垂线,垂足分别为D,E,
则△ADN∽△NEB,
∴
 ,
,
∴
 =
=
 ,
,
∴
 (x1x2)2=﹣(3﹣x1)(3﹣x2),
(x1x2)2=﹣(3﹣x1)(3﹣x2),
 (x1x2)2=﹣[9﹣3(x1+x2)+x1x2],
(x1x2)2=﹣[9﹣3(x1+x2)+x1x2],
又∵由l:y=kx+2,抛物线y=
 x2,得:
x2,得:
 x2﹣kx﹣2=0,
x2﹣kx﹣2=0,
∴x1+x2=4k,x1x2=﹣8,
∴
 (﹣8)2=﹣[9﹣3×4k﹣8],
(﹣8)2=﹣[9﹣3×4k﹣8],
∴k=
 ;
;
设直线AO的解析式为y=mx,
∵过A(x1,
 x12),
x12),
∴
 x12=mx1,
x12=mx1,
∴m=
 x1,
x1,
∴直线AO的解析式为y=
 x1x,
x1x,
∵BC∥y轴,直线BC的解析式为x=x2,
∴C(x2,
 x1x2),
x1x2),
又∵由(1)知x1x2=﹣8,
∴C(x2,﹣2),
又∵x2>0,
∴C点一定在没有端点的射线y=﹣2(x>0)上运动,
∴由轴对称可知:△MNC的周长的最小值为3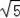
 +
+
 .
.


【点评】本题考查了二次函数的综合知识,题目中往往设出有关点的坐标,根据题意得到方程,从而求得点的坐标的方法在解决此类题目中应用十分的广泛,在求有关动点问题时要注意分析题意分情况讨论结果.




 ,计算:
,计算:
 ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+(
 )﹣1的值.
)﹣1的值.
