题目内容
一个不透明的布袋里装有4个兵乓球,每个求上面分别标有1、2、3、4,从布袋中随机摸取一个兵乓球,记下数字
(1)若将第一次摸取的兵乓球放回后,摇匀,再随机摸取第二个兵乓球,记下数字
①请你用树状图或列表法列出所有可能的结果;
②求“两次记下的数字之和大于4且小于7”的概率;
(2)若将第一次摸取的兵乓球记下数字后不放回,再随机摸取第二个兵乓球并记下数字,请直接写出“两次记下的数字之和大于4且小于7”的概率.
【考点】列表法与树状图法.
【分析】(1)根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.使用列表法分析时,一定要做到不重不漏.
(2)依据题意先用列表法或画树状图法分析所有等可能和达到某种效果的可能,然后根据概率公式求出该事件的概率.
【解答】解:(1)①列表如下,
|
| 1 | 2 | 3 | 4 |
| 1 | 1,1 | 1,2 | 1,3 | 1,4 |
| 2 | 2,1 | 2,2 | 2,3 | 2,4 |
| 3 | 3,1 | 3,2 | 3,3 | 3,4 |
| 4 | 4,1 | 4,2 | 4,3 | 4,4 |
②∵由表可知,共有16个等可能的结果,“两次记下的数字之和大于4且小于7”的有7次,
∴P(两次记下的数字之和大于4且小于7)=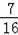
 ;
;
(2)根据题意画树形图如下:
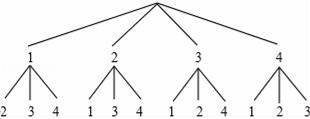

由以上可知共有12种可能结果分别为:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3);“两次记下的数字之和大于4且小于7”的有(1,4),(2,3),(2,4),(3,2),(4,1),(4,2)6种,
故P(两次记下的数字之和大于4且小于7)=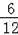
 =
=
 ;.
;.
【点评】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.

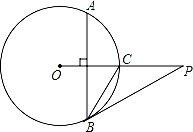
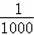
 x2+
x2+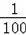
 x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.


 B.
B.
 C.
C.
 D.
D.

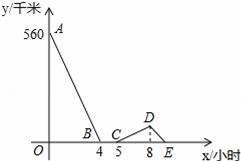


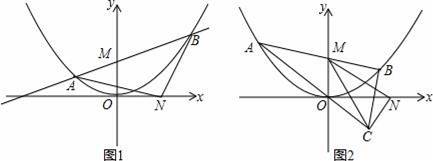

 B.
B.  C.
C. D.
D.
 的单价各为多少元?(8分)
的单价各为多少元?(8分)