题目内容
3．计算及解方程：（1）（$\sqrt{3}$-1）0-（-$\frac{1}{2}$）-2+$\sqrt{9}$
（2）（x-5）3=-64；
（3）2x2-128=0．
分析 （1）原式利用零指数幂、负整数指数幂法则，以及算术平方根定义计算即可得到结果；
（2）方程利用立方根定义计算即可求出x的值；
（3）方程整理后，利用平方根定义计算即可求出x的值．
解答 解：（1）原式=1-4+3=0；
（2）方程开立方得：x-5=-4，
解得：x=1；
（3）x2=64，
开方得：x=8或x=-8．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
13．若二次函数y=ax2的图象过点P（-1，3），则该图象必经过点（ ）
| A． | （3，-1） | B． | （1，3） | C． | （-3，1） | D． | （-1，-3） |
11．不在抛物线y=x2-3的图象上的点是（ ）
| A． | （1，-2） | B． | （-2，1） | C． | （0，-3） | D． | （1，2） |
18．
已知实数a、b在数轴上表示的点如图，化简|a+b|+$\sqrt{{{（a-b+1）}^2}}$的结果为（ ）
已知实数a、b在数轴上表示的点如图，化简|a+b|+$\sqrt{{{（a-b+1）}^2}}$的结果为（ ）| A． | 2b-1 | B． | 2a+1 | C． | -2a-1 | D． | -2b+1 |
13．
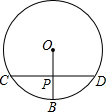如图，CD垂直平分半径OB，垂足为P点，CD=12，则OB=（ ）
如图，CD垂直平分半径OB，垂足为P点，CD=12，则OB=（ ）| A． | 2$\sqrt{3}$ | B． | 4$\sqrt{3}$ | C． | 4$\sqrt{5}$ | D． | 8$\sqrt{3}$ |