题目内容
18. 已知实数a、b在数轴上表示的点如图,化简|a+b|+$\sqrt{{{(a-b+1)}^2}}$的结果为( )
已知实数a、b在数轴上表示的点如图,化简|a+b|+$\sqrt{{{(a-b+1)}^2}}$的结果为( )| A. | 2b-1 | B. | 2a+1 | C. | -2a-1 | D. | -2b+1 |
分析 先根据数轴得出a<0<b,且|a|<|b|,进而利用二次根式的性质和绝对值的性质化简得出即可.
解答 解:由题意,可得a<0<b,且|a|<|b|,
所以|a+b|+$\sqrt{{{(a-b+1)}^2}}$=a+b+b-a-1=2b-1.
故选A.
点评 此题主要考查了实数与数轴,二次根式的性质与化简,绝对值的性质,正确化简是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知代数式x+2y的值是6,则代数式4x+8y-1的值是( )
| A. | 21 | B. | 22 | C. | 23 | D. | 25 |
13.已知⊙O的直径为10cm,点A到圆心O的距离为4,则经过点A的所以弦中,最短的弦的长为( )
| A. | 5cm | B. | 10cm | C. | 6cm | D. | 8cm |
7. 如图,直线l∥m∥n,等边三角形ABC的顶点B,C分别在直线n和m上,边BC与直线n的夹角为20°,则∠α的度数为( )
如图,直线l∥m∥n,等边三角形ABC的顶点B,C分别在直线n和m上,边BC与直线n的夹角为20°,则∠α的度数为( )
 如图,直线l∥m∥n,等边三角形ABC的顶点B,C分别在直线n和m上,边BC与直线n的夹角为20°,则∠α的度数为( )
如图,直线l∥m∥n,等边三角形ABC的顶点B,C分别在直线n和m上,边BC与直线n的夹角为20°,则∠α的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
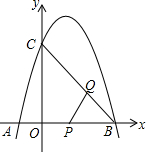 如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于C点.动点P从点B出发,沿x轴负方向以每秒1个单位的速度运动.过点P作PQ⊥BC,垂足为Q,再将△PBQ绕点P按逆时针方向旋转90°.设点P的运动时间为t秒.
如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于C点.动点P从点B出发,沿x轴负方向以每秒1个单位的速度运动.过点P作PQ⊥BC,垂足为Q,再将△PBQ绕点P按逆时针方向旋转90°.设点P的运动时间为t秒.