题目内容
13.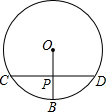 如图,CD垂直平分半径OB,垂足为P点,CD=12,则OB=( )
如图,CD垂直平分半径OB,垂足为P点,CD=12,则OB=( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 8$\sqrt{3}$ |
分析 连接OD,先根据垂径定理求出DE的长,再设AB=4x,则OE=x,OD=2x,根据勾股定理求出x的值即可.
解答 解:连接OD,
∵弦CD垂直平分半径OB,垂足为P,CD=12,
∴DP=$\frac{1}{2}$CD=6,
设OP=x,OD=2x,
∴OP2+DP2=OD2,即x2+62=(2x)2,解得x=2$\sqrt{3}$,
∴OB=OD=4$\sqrt{3}$.
故选B.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
1.已知三个数2,$\sqrt{2}$,4.如果再添加一个数,就得到这四个数成比例了,则添加的数是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$或$\frac{\sqrt{2}}{2}$ | C. | 2$\sqrt{2}$,4$\sqrt{2}$或8$\sqrt{2}$ | D. | 2$\sqrt{2}$,$\frac{\sqrt{2}}{2}$或4$\sqrt{2}$ |
18.下列命题是真命题的是( )
| A. | 有一个角相等的两个等腰三角形相似 | |
| B. | 两边对应成比例且有一个角相等的两个三角形相似 | |
| C. | 四个内角都对应相等的两个四边形相似 | |
| D. | 斜边和一条直角边对应成比例的两个直角三角形相似 |
3.袋子中装有2个红球、3个白球和3个黄球,这些球除颜色外无其他差别,从袋子中随机摸出一个球,是白球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |