题目内容
14.如图,在△ABC中,∠ACB=90°,CA=CB,点P在△ABC内,且PA=3,PB=1,PC=2,求△CPB的度数.小东同学尝试在CP的右侧作CD⊥CP,并截取CD=CP,再连接DP、DB,使问题获解:小西同学把CD画在CP的左侧,同样也使问题获解,请你分别在下面的两个图中画出小东和小西想到的辅助线,并选择其中的一种写出解答.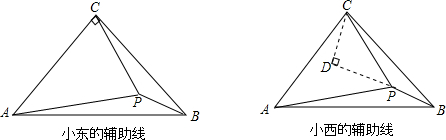
分析 小东的辅助线:根据SAS证明△CAP与△CBD全等即可,利用勾股定理的逆定理得出△PDB是直角三角形,进而解答即可;
小西的辅助线:同理证得△ADC≌△BPC,利用勾股定理的逆定理得出△ADP是直角三角形,进而解答即可.
解答 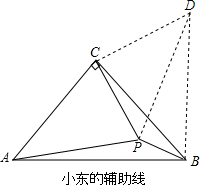 解:(1)作CD⊥CP,并截取CD=CP,再连接DP、DB,
解:(1)作CD⊥CP,并截取CD=CP,再连接DP、DB,
∵∠ACB=90°,CD⊥PC,
∴∠ACB=∠PCD=90°,
∴∠ACP=∠BCD,
在△CAP与△CBD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCD}\\{PC=CD}\end{array}\right.$,
∴△CAP≌△CBD,
∴PA=BD=3,
∵PC=CD=2,CD⊥PC,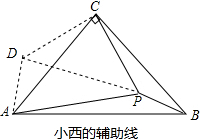
∴DP=$\sqrt{P{C}^{2}+C{D}^{2}}$,∠CPD=45°
∴DP2=8=BD2-PB2=32-12=8,
∴△BDP是直角三角形,
∴∠DPB=90°,
∴∠BPC=∠DPB+∠CPD=135°;
过C作CD⊥PC,使CD=PC,连接AD,CD PD,
同理△ADC≌△BPC,
∴AD=PB=1,∠PC=∠ADC,
∵PD=$\sqrt{2}$PC=2$\sqrt{2}$,
∴AD2+PD2=12+(2$\sqrt{2}$)2=9=AP2,
∴∠ADP=90°,
∴∠ADC=135°,
∴∠BPC=135°.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理的逆定理,根据SAS证得三角形全等是解题的关键.

练习册系列答案
相关题目
2.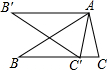 如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )
如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )
 如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )
如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )| A. | 10° | B. | 20° | C. | 30° | D. | 45° |
19. 据悉,沙坪坝火车站改造工程预计于2015年完工并投入使用,到时可有效解决三峡广场堵车问题.现有甲、乙两工程队分别同时修建两条600米长的道路,已知修建道路长度y(米)与修建时间x(天)之间的关系如图所示,则下列说法中错误的是( )
据悉,沙坪坝火车站改造工程预计于2015年完工并投入使用,到时可有效解决三峡广场堵车问题.现有甲、乙两工程队分别同时修建两条600米长的道路,已知修建道路长度y(米)与修建时间x(天)之间的关系如图所示,则下列说法中错误的是( )
 据悉,沙坪坝火车站改造工程预计于2015年完工并投入使用,到时可有效解决三峡广场堵车问题.现有甲、乙两工程队分别同时修建两条600米长的道路,已知修建道路长度y(米)与修建时间x(天)之间的关系如图所示,则下列说法中错误的是( )
据悉,沙坪坝火车站改造工程预计于2015年完工并投入使用,到时可有效解决三峡广场堵车问题.现有甲、乙两工程队分别同时修建两条600米长的道路,已知修建道路长度y(米)与修建时间x(天)之间的关系如图所示,则下列说法中错误的是( )| A. | 甲队每天修建100米 | B. | 第6天,甲队比乙队多修建100米 | ||
| C. | 乙队开工两天后,每天修建50米 | D. | 甲队比乙队提前3天完成任务 |
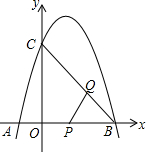 如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于C点.动点P从点B出发,沿x轴负方向以每秒1个单位的速度运动.过点P作PQ⊥BC,垂足为Q,再将△PBQ绕点P按逆时针方向旋转90°.设点P的运动时间为t秒.
如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于C点.动点P从点B出发,沿x轴负方向以每秒1个单位的速度运动.过点P作PQ⊥BC,垂足为Q,再将△PBQ绕点P按逆时针方向旋转90°.设点P的运动时间为t秒.