题目内容
13.若二次函数y=ax2的图象过点P(-1,3),则该图象必经过点( )| A. | (3,-1) | B. | (1,3) | C. | (-3,1) | D. | (-1,-3) |
分析 先把P点坐标代入y=ax2求出a=3,则抛物线解析式为y=3x2,然后计算自变量为3,1,-3,-1所对应的函数值,再根据二次函数图象上点的坐标特征进行判断.
解答 解:把P(-1,3)代入y=ax2得a=3,
所以抛物线解析式为y=3x2,
当x=3时,y=27;当x=1时,y=3;当x=-3时,y=27;当x=-1时,y=3,
所以点(1,3)在抛物线上.
故选B.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.解决此题的关键是把图象上的点的坐标代入解析式求出a的值.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1.如果a>b,那么下列结论一定正确的是( )
| A. | a-3<b-3 | B. | 1+a>1+b | C. | -3a>-3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
8.已知代数式x+2y的值是6,则代数式4x+8y-1的值是( )
| A. | 21 | B. | 22 | C. | 23 | D. | 25 |
2.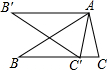 如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )
如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )
 如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )
如图,在△ABC中,AB=BC,将△ABC绕顶点A顺时针旋转一个角度后,恰好使AB′∥BC.若∠B=20°,则△ABC旋转了( )| A. | 10° | B. | 20° | C. | 30° | D. | 45° |
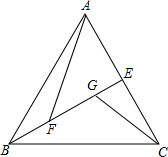 如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,
如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,