题目内容
18. 二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c的部分对应值如下表:| x | … | -3 | -2 | 0 | 1 | 3 | 4 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 0 | 7 | … |
(2)直接写出二次函数的对称轴x=1,顶点坐标(1,-9),与x轴的交点(-2,0)、(4,0),与y轴的交点(0,-8);
(3)画出这个二次函数的图象,利用图象直接写出当x为何值时,y>0.
分析 (1)把(-2,0),(3,-5),(0,-8)代入y=ax2+bx+c中,根据待定系数法即可求得;
(2)利用表格求得对称轴、顶点坐标,利用表格得出与x轴、y轴的交点坐标即可;
(3)画出函数图象,结合图象得出答案即可.
解答 解:(1)把(-2,0),(3,-5),(0,-8)代入y=ax2+bx+c得
$\left\{\begin{array}{l}{4a-2b+c=0}\\{9a+3b+c=-5}\\{c=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-8}\end{array}\right.$,
因此二次函数的解析式为y=x2-2x-8;
(2)由表格可知二次函数的对称轴x=1,顶点坐标(1,-9),与x轴的交点(-2,0)、(4,0),与y轴的交点(0,-8);
(3)画出这个二次函数的图象如下:
当x为何值时,x<-2或x>4时,y>0.
点评 本题考查了二次函数的性质,待定系数法求二次函数的解析式,以及二次函数的对称性求顶点坐标、对称轴与x轴、y轴的交点坐标,熟练掌握待定系数法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.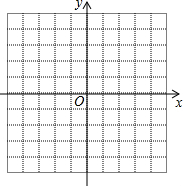 已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).
已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).