题目内容
17. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )| A. | 0<AD<3 | B. | 1≤AD<$\frac{5}{2}$ | C. | $\frac{15}{7}$≤AD<$\frac{5}{2}$ | D. | $\frac{15}{8}$≤AD<$\frac{5}{2}$ |
分析 首先由Rt△ABC中,∠C=90°,AC=3,BC=4,可求得AB的长,然后根据题意画出图形,分别从当⊙D与BC相切时与当⊙D与BC相交时,去分析求解即可求得答案.
解答 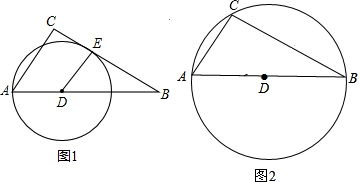 解:∵Rt△ABC中,∠C=90°,AC=3,BC=4,
解:∵Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
以D为圆心,AD的长为半径画⊙D,
①如图1,当⊙D与BC相切时,DE⊥BC时,
设AD=x,则DE=AD=x,BD=AB-AD=5-x,
∵∠BED=∠C=90°,∠B是公共角,
∴△BDE∽△BAC,
∴$\frac{BD}{AB}=\frac{DE}{AC}$,
即$\frac{5-x}{5}=\frac{x}{3}$,
解得:x=$\frac{15}{8}$;
②如图2,当⊙D与BC相交时,若交点为B或C,则AD=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴AD的取值范围是$\frac{15}{8}$≤AD<$\frac{5}{2}$.
故选D.
点评 此题考查了点与圆的位置关系、勾股定理以及相似三角形的判定与性质.注意根据题意画出图形,结合图形求解是关键.

练习册系列答案
相关题目
2.计算$\sqrt{\frac{2}{3}}$÷$\sqrt{\frac{3}{2}}$的结果是( )
| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{2}{3}$ |
 问题情境:我们知道,两边及其中一边所对的角分别对应相等的两个三角形不一定全等,那么在什么情况下,这样的两个三角形才全等呢?为了研究这个问题,我们先思考下面几个问题:
问题情境:我们知道,两边及其中一边所对的角分别对应相等的两个三角形不一定全等,那么在什么情况下,这样的两个三角形才全等呢?为了研究这个问题,我们先思考下面几个问题:
 如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动;同时一动点Q从点D出发,以每秒3个单位长度的速度沿DO向点O运动,运动到点O停止,点Q与点P同时停止.
如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动;同时一动点Q从点D出发,以每秒3个单位长度的速度沿DO向点O运动,运动到点O停止,点Q与点P同时停止.
 如图,已知二次函数y=-x2-3x+4的图象与x轴的交于A,B两点,与y轴交于点C.一次函数的图象过点A、C.
如图,已知二次函数y=-x2-3x+4的图象与x轴的交于A,B两点,与y轴交于点C.一次函数的图象过点A、C.