题目内容
7.现有一个正六边形的纸片,该纸片的边长为20cm,张萌想用一张圆形纸片将该正六边形纸片完全覆盖住,则圆形纸片的直径不能小于40cm.分析 根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB的度数,最后根据等腰三角形及直角三角形的性质解答即可.
解答 解:如图所示,正六边形的边长为20cm,OG⊥BC,
∵六边形ABCDEF是正六边形,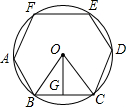
∴∠BOC=$\frac{360°}{6}$=60°,
∵OB=OC,OG⊥BC,
∴∠BOG=∠COG=$\frac{1}{2}$=30°,
∵OG⊥BC,OB=OC,BC=20cm,
∴BG=$\frac{1}{2}$BC=$\frac{1}{2}$×20=10cm,
∴OB=$\frac{BG}{sin30°}$=$\frac{10}{\frac{1}{2}}$=20cm,
∴圆形纸片的直径不能小于40cm;
故答案为:40.
点评 本题考查的是正多边形和圆,根据题意画出图形,利用直角三角形的性质及正六边形的性质解答是解答此题的关键.

练习册系列答案
相关题目
17. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )| A. | 0<AD<3 | B. | 1≤AD<$\frac{5}{2}$ | C. | $\frac{15}{7}$≤AD<$\frac{5}{2}$ | D. | $\frac{15}{8}$≤AD<$\frac{5}{2}$ |
16. 如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
 如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )| A. | 过一点有无数条直线 | |
| B. | 两点之间线段的长度,叫做这两点之间的距离 | |
| C. | 两点确定一条直线 | |
| D. | 两点之间,线段最短 |
17. △ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )
△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )
 △ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )
△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )| A. | (5,-2) | B. | (-5,-2) | C. | (-2,-5) | D. | (-2,5) |

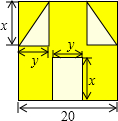 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
 +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6 如图,OE为∠AOD的平分线,∠COD=$\frac{1}{4}$∠EOC,∠COD=15°,求∠AOD的大小.
如图,OE为∠AOD的平分线,∠COD=$\frac{1}{4}$∠EOC,∠COD=15°,求∠AOD的大小.