题目内容
4.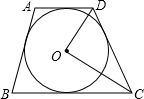 如图所示,在⊙O的外切梯形ABCD中,若AD∥BC,则∠DOC的大小是( )
如图所示,在⊙O的外切梯形ABCD中,若AD∥BC,则∠DOC的大小是( )| A. | 45° | B. | 60° | C. | 70° | D. | 90° |
分析 先由平行线的性质得同旁内角互补:∠ADC+∠BCD=180°,由切线长定理得:OD平分∠ADC,OC平分∠BCD,所以∠ODC+∠OCD=90°,根据三角形的内角和得:∠DOC=90°.
解答 解:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵梯形ABCD内切于圆O,
∴OD平分∠ADC,OC平分∠BCD,
∴∠ODC=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}$∠BCD,
∴∠ODC+∠OCD=$\frac{1}{2}$∠ADC+$\frac{1}{2}$∠BCD=$\frac{1}{2}$×180°=90°,
∴∠DOC=90°,
故选D.
点评 本题考查了梯形的内切圆和平行线的性质,熟知圆外一点引圆的两条切线,这点与圆心的连线平分切线所成的夹角;此题是常考题型,两对角平分线构成直角三角形,要熟练掌握.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.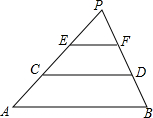 如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )
如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )
 如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )
如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )| A. | 18 | B. | 16 | C. | 12 | D. | 10 |
9.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 一个三角形只有一个外接圆 | |
| C. | 和半径垂直的直线是圆的切线 | |
| D. | 三角形的外心到三角形三边的距离相等 |
16.下列不一定是相似图形的是( )
| A. | 边数相同的正多边形 | B. | 两个等腰直角三角形 | ||
| C. | 两个圆 | D. | 两个等腰三角形 |