题目内容
4.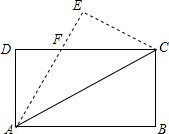 如图,把长方形ABCD纸片沿AC翻折,三角形ABC被翻折到三角形AEC位置,AE与CD相交于点F
如图,把长方形ABCD纸片沿AC翻折,三角形ABC被翻折到三角形AEC位置,AE与CD相交于点F(1)判断∠FAC与∠FCA的大小关系,说明理由;
(2)在图形中找出一个与∠DAF相等的角并说出相等的理由.
分析 (1)由翻折的性质可知∠BAC=∠FAC,由平行线的性质可知∠FCA=∠BAC,从而可证明∠FAC=∠FCA;
(2)由平行线的性质可知∠DAC=∠BCA,由翻折的性质可知∠ECA=∠BCA,由等式的性质可得到∠ECF=∠DAF.
解答 解:(1)相等.
理由:由翻折的性质可知;∠BAC=∠FAC.
又∵四边形ABCD为长方形,
∴DC∥AD.
∴∠FCA=∠BAC.
∴∠FAC=∠FCA.
(2)∠ECF=∠DAF.
∵四边形ABCD为长方形,
∴DA∥BC.
∴∠DAC=∠BCA.
由翻折的性质可知∠ECA=∠BCA.
∴∠DAC=∠ECA.
∴∠DAC-∠FAC=∠ECA-∠FCA.
∴∠ECF=∠DAF.
点评 本题主要考查的是翻折的性质和矩形的性质、掌握翻折的性质和平行线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.某班为了奖励在校运会上获得好成绩的运动员,花了200元钱购买甲乙两种奖品共30件,其中甲种奖品8元/件,乙种奖品6元/件.若设购买甲种奖品x件,乙种奖品y件,则所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{8x+6y=30}\\{x+y=200}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+8y=30}\\{x+y=200}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=30}\\{8x+6y=200}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=30}\\{6x+8y=200}\end{array}\right.$ |
12.若关于x的方程$\frac{ax}{x-2}$=$\frac{4}{x-2}$+1无解,则a的值是( )
| A. | 5 | B. | -5 | C. | -4 | D. | 2 |
14.三角形的两边长分别为6cm和10cm,则下列长度的四条线段中能作为第三边的是( )
| A. | 17cm | B. | 16cm | C. | 4cm | D. | 5cm |
 如图,AD、AE分别是△ABC的高和角平分线,∠C=36°,∠B=72°,则∠DAE的度数为18°(度).
如图,AD、AE分别是△ABC的高和角平分线,∠C=36°,∠B=72°,则∠DAE的度数为18°(度). 在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AD=3,BD=1.则∠ABC的度数为60°度.
在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AD=3,BD=1.则∠ABC的度数为60°度.