题目内容
9. 如图,AD、AE分别是△ABC的高和角平分线,∠C=36°,∠B=72°,则∠DAE的度数为18°(度).
如图,AD、AE分别是△ABC的高和角平分线,∠C=36°,∠B=72°,则∠DAE的度数为18°(度).
分析 首先根据三角形的内角和定理,求出∠BAC的度数是多少;然后根据AE是△ABC的角平分线,求出∠EAC的度数是多少;最后在Rt△ACD中,求出∠CAD的度数,即可求出∠DAE的度数.
解答 解:∵∠B=72°,∠C=36°,
∴∠BAC=180°-∠B-∠C=72°,
∵AE是△ABC的角平分线,
∴∠EAC=72°÷2=36°,
∵AD⊥BC,
∴∠CAD=90°-∠C=90°-36°=54°,
∴∠DAE=∠DAC-∠CAE
=54°-36°
=18°,
即∠DAE的度数是18°.
故答案为:18°.
点评 此题主要考查了三角形的内角和定理,三角形的角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:三角形内角和是180°.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
17.七位评委对参加普通话比赛的选手评分,比赛规则规定要去掉一个最高分和一个最低分,然后计算剩下了5个分数的平均分作为选手的比赛分数,规则“去掉一个最高分和一个最低分”一定不会影响这组数据的( )
| A. | 平均数 | B. | 中位数 | C. | 极差 | D. | 众数 |
1.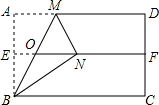 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
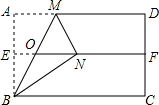 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
19.下列命题是真命题的是( )
| A. | 明天我市降雨的概率是60%,指的是有60%的时间在下雨 | |
| B. | 样本的方差可以近似地反映总体的分布规律 | |
| C. | 若一组数据2,3,5,a的平均数是3,则这组数据的众数和中位数都是3 | |
| D. | 数据2,5,4,9的方差是6.5 |
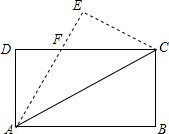 如图,把长方形ABCD纸片沿AC翻折,三角形ABC被翻折到三角形AEC位置,AE与CD相交于点F
如图,把长方形ABCD纸片沿AC翻折,三角形ABC被翻折到三角形AEC位置,AE与CD相交于点F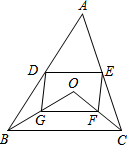 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.