Question

17．如图，在△ABC中，点D在∠ACB的平分线上，过点D作BC的平行线与∠ACB的外角平分线相交于点E，DE交AC于点F
（1）判断△CDE的形状，并说明理由；
（2）判断DF与EF的大小关系，并说明理由；
（3）若调整点D的位置，使DE与CA的延长线相交于点F，（2）中结论成立吗？

Answer 1

分析 （1）结论：△CDE是直角三角形，只要证明∠DCE=90°即可．
（2）结论：DF=EF．只要证明DF=FC，FC=EF即可．
（3）结论仍然成立，理由类似（2）．

解答 解：（1）结论：△CDE是直角三角形．
理由：∵∠DCB=∠DCA，∠ECF=∠ECG，
∴∠ECD=$\frac{1}{2}$（∠ACB+∠ACG）=90°，
∴△EDC是直角三角形．

（2）结论：DF=EF．
理由：∵DE∥BC，
∴∠FDC=∠DCB，∠E=∠ECG，
∵∠DCB=∠DCA，∠ECA=∠ECG，
∴∠FDC=∠FCD，∠E=∠FCE，
∴DF=FC，FC=EF，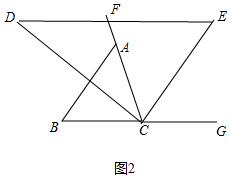
∴DF=EF．

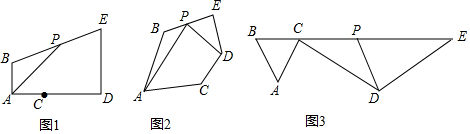
（3）如图2中，结论仍然成立：DF=EF．
理由：∵DE∥BC，
∴∠FDC=∠DCB，∠E=∠ECG，
∵∠DCB=∠DCA，∠ECA=∠ECG，
∴∠FDC=∠FCD，∠E=∠FCE，
∴DF=FC，FC=EF，
∴DF=EF．

点评 本题考查等腰三角形的性质、平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于基础题，中考常考题型．