题目内容
15.解不等式组:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$,并把解集在数轴上表示出来,并判断$\sqrt{3}$是否为不等式组的一个解.分析 先求出不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x>-2,
∴不等式组的解集为-2<x≤1,
在数轴上表示不等式组的解集为: ,
,
∵$\sqrt{3}$>1,
∴$\sqrt{3}$不是不等式组的解.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,估算无理数的大小的应用,解此题的关键是能根据找不等式组解集的规律找出不等式组的解集.

练习册系列答案
相关题目
5.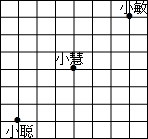 课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
 课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )| A. | (5,4) | B. | (4,4) | C. | (3,4) | D. | (4,3) |
3.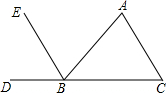 如图,所给条件:①∠C=∠ABE,②∠C=∠DBE,③∠A=∠ABE,④∠CBE+∠C=180°中,能判定BE∥AC的条件有( )
如图,所给条件:①∠C=∠ABE,②∠C=∠DBE,③∠A=∠ABE,④∠CBE+∠C=180°中,能判定BE∥AC的条件有( )
 如图,所给条件:①∠C=∠ABE,②∠C=∠DBE,③∠A=∠ABE,④∠CBE+∠C=180°中,能判定BE∥AC的条件有( )
如图,所给条件:①∠C=∠ABE,②∠C=∠DBE,③∠A=∠ABE,④∠CBE+∠C=180°中,能判定BE∥AC的条件有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
10.如果2m,0,1-m这三个实数在数轴上所对应的点从左到右依次排列,那么m的取值范围是( )
| A. | m>0 | B. | m>0.5 | C. | m<0 | D. | 0<m<0.5 |
5. 某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
(1)根据实际需要,将阅读能力、科研能力、组织能力三项测试得分按5:3:2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.
 某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)| 项目 人员 | 教学能力 | 科研能力 | 组织能力 |
| 甲 | 86 | 93 | 73 |
| 乙 | 81 | 95 | 79 |
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.
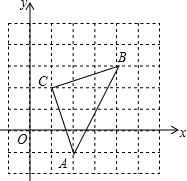 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1).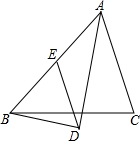 在△ABC中,AD平分∠BAC.BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.
在△ABC中,AD平分∠BAC.BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.