题目内容
7.(1)解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x}\\{1-3(x-1)<8-x}\end{array}\right.$,并把其解集在数轴上表示出来.(2)已知x,y满足(2014-x)2+|y-2015|=0,求[(x-y)2+(x+y)(x-y)]÷2x的值.
分析 (1)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
(2)先求出x、y的值,再算乘法,合并同类项,算除法,最后代入求出即可.
解答 解:(1)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x①}\\{1-3(x-1)<8-x②}\end{array}\right.$
∵解不等式①得:x≤3,
解不等式②得:x>-2,
∴不等式组的解集为-2<x≤3,
在数轴上表示不等式组的解集为: ;
;
(2)(2014-x)2+|y-2015|=0,
2014-x=0,y-2015=0,
x=2014,y=2015,
[(x-y)2+(x+y)(x-y)]÷2x
=[x2-2xy+y2+x2-y2]÷2x
=[2x2-2xy]÷2x
=x-y
=2014-2015
=-1.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,整式的混合运算和求值的应用,能求出不等式组的解集是解(1)小题的关键,能正确运用整式的运算法则进行化简是解(2)小题的关键,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 如图,要使输出值y大于100,则输入的最小正整数x的值是( )
如图,要使输出值y大于100,则输入的最小正整数x的值是( )
 如图,要使输出值y大于100,则输入的最小正整数x的值是( )
如图,要使输出值y大于100,则输入的最小正整数x的值是( )| A. | 22 | B. | 21 | C. | 20 | D. | 以上答案都不对 |
2.小明在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为4a2■ab+9b2,则中间一项的系数是( )
| A. | 12 | B. | -12 | C. | 12或-12 | D. | 36 |
12.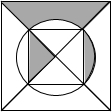 在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )
在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )
 在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )
在如图所示的正方形和圆形组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
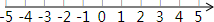 解不等式组$\left\{\begin{array}{l}{x>\frac{x-1}{2}①}\\{2(x+3)>3x+2②}\end{array}\right.$,并将它的解集表示在如图所示的数轴上.
解不等式组$\left\{\begin{array}{l}{x>\frac{x-1}{2}①}\\{2(x+3)>3x+2②}\end{array}\right.$,并将它的解集表示在如图所示的数轴上. 如图所示,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上.若∠1=25°,则∠2的度数为20°.
如图所示,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上.若∠1=25°,则∠2的度数为20°.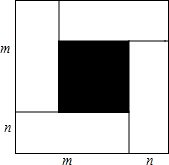 如图,大正方形由四个相同的长方形和一个小正方形组成,设长方形的两边长为m,n(m>n),大小正方形的边长分别为x,y.观察图案,指出以下关系式:①x2-y2=4mn;②m2-n2=xy;③2n2=(x-y)2;④m2+n2=$\frac{{x}^{2}+{y}^{2}}{2}$,其中正确的是①②④(写出正确结论的序号)
如图,大正方形由四个相同的长方形和一个小正方形组成,设长方形的两边长为m,n(m>n),大小正方形的边长分别为x,y.观察图案,指出以下关系式:①x2-y2=4mn;②m2-n2=xy;③2n2=(x-y)2;④m2+n2=$\frac{{x}^{2}+{y}^{2}}{2}$,其中正确的是①②④(写出正确结论的序号)