题目内容
9.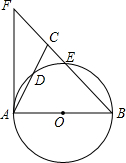 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.(1)求证:∠ABC=2∠CAF;
(2)若AC=2$\sqrt{10}$,CE:EB=1:4,求CE的长.
分析 (1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2$\sqrt{10}$)2=x2+(3x)2求得答案.
解答 (1)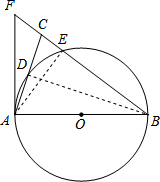 证明:如图,连接BD.
证明:如图,连接BD.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°.
∵AF是⊙O的切线,
∴∠FAB=90°,
即∠DAB+∠CAF=90°.
∴∠CAF=∠ABD.
∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.
∴∠ABC=2∠CAF.
(2)解:如图,连接AE,
∴∠AEB=90°,
设CE=x,
∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x,
在Rt△ACE中,AC2=CE2+AE2,
即(2$\sqrt{10}$)2=x2+(3x)2,
∴x=2.
∴CE=2.
点评 本题主要考查了切线的性质、三角函数以及勾股定理,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用是解答此题关键.

练习册系列答案
相关题目
1.要使二次根式$\sqrt{x-2}$有意义,x必须满足( )
| A. | x≤2 | B. | x≥2 | C. | x>2 | D. | x<2 |
18.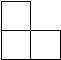 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
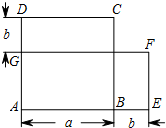 (1)如图,正方形ABCD的边长为a,周长为4a;长方形AEFG的长为a+b,宽为a-b,长为4a.
(1)如图,正方形ABCD的边长为a,周长为4a;长方形AEFG的长为a+b,宽为a-b,长为4a.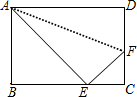 如图所示,将矩形ABCD沿直线AF折叠,点D恰好落在边BC上的点E处,若AB=8cm,BC=10cm,求EF的长.
如图所示,将矩形ABCD沿直线AF折叠,点D恰好落在边BC上的点E处,若AB=8cm,BC=10cm,求EF的长.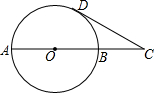 如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.
如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.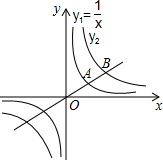 如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.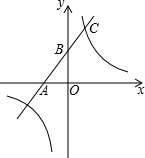 如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.